Dante’s Use of Logic in the Monarchia

“Intemptatas ab aliis ostendere veritates”:
Dante’s use of logic in the Monarchia

Stefano Pelizzari, University of Milan (2020)

The following presentation was prepared on the occasion of the seminar ‘A morning on Dante and Logic’ held on February 28, 2020, upon the supportive and creative initiative of Professor Teodolinda Barolini.

It shares some preliminary results of the doctoral research about ‘The logical terminology of Dante Alighieri’s Monarchia’ that I am carrying out at the Department of Philosophy of the University of Milan (2018-2021), and that I was able to further develop as a Visiting Scholar at the Department of Italian of Columbia University (2019-2020) thanks to the generous support of the Associazione Amici di Claudio Demattè.

The goal of this essay is not just to illustrate Dante’s familiarity with the more cutting-edge trends in logic from the 13th and the early 14th centuries, but also to promote further discussion about how logic and scientific methodology contribute to create a specific kind of authorship in the context of the Monarchia.

The essay deals with some of the most representative and exemplary passages of the treatise without going into specifics and relying in good part on the existing literature on the subject. In particular, I have focused on Dante’s acquaintance with some relevant properties of the so-called ‘syncategorematic’ terms (i.e. functional words such as ‘all’; ‘none’; ‘only’; ‘nothing except’; cf. Lambertini 2011) and on his accurate knowledge of the technical rules of the ‘consequences’, a branch of logical analysis that spread in Europe starting from the early 14th century (Mozzillo-Howell 1998; 2012). By contrast, I have not attended to Dante’s deployment of the Aristotelian fallacies in Book III, and I have held back from pointing out explicitly all the numerous ties with Peter of Spain’s Tractatus, as they were extensively treated by Bruno Nardi in his Ricciardi edition of the Monarchia (Nardi 1979).

Furthermore, I list some passages in which Dante seems to make a ‘poietic’ use of logic, i.e. occasions in which the language of the syllogism is deliberately employed to create metaphors and similes. Three paradigmatic examples are presented: the description of the relationship between the universal monarch and local princes (Book I, Ch. xiv); the characterization of the goal of humanity in terms of a necessary means to achieve the universal goal of Nature (Book II, Ch. vi); and the comparison between the two beatitudes and two syllogistic conclusions to be reached through different means (Book III, Ch. xvi).

Finally, I attempt to answer the following question: why do we find such a massive and exhibited use of logic in a political treatise like the Monarchia? I suggest a threefold answer. First, because the Monarchia is overtly more than a political treatise: it is intended to be a prophetic and scientific revelation, capable of inducing a general liberation of the human race in virtue of the irrefutability of its demonstrations. Second, because Dante was fully aware that his major opponents were, as Cassell notes, “towering experts in the field of logic”: therefore, it was crucial to expose their “regnar per forza e per sofismi” (Par. XI, 5) through an adequate and commensurate deployment of technical tools. Finally, because Dante, as an author, endeavors to distinguish himself from two different professional categories of his time: on the one side, the decretalisti, papist legisti who dealt with politics but sine arte, i.e. without scientific rigor and method; and, at the other extreme, all those who treated logic – especially in the university environments – as a completely autonomous subject, detaching themselves from what Dante calls with technical terminology the “importatum per verba” (Book I, Ch. Xii), the actual meaning conveyed by words.

–Stefano Pelizzari, University of Milan

1. Introduction
2. The truth that sets humanity free
3. Dante’s ‘technical’ use of logic
3.1. Monarchia I, xi: Dante and the Syncategoremata
**3.2. Monarchia III, viii: Dante and the ‘proprietas terminorum’
3.3 Dante and the language of the ‘consequentiae’
4. Dante’s ‘poietic’ use of logic
5. Dante’s ‘exhibited’ use of logic and the creation of an authorship
References**

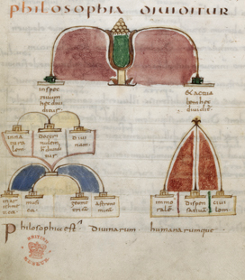
MS BL Harley 2637, f. 15v, The Seven Liberal Arts, Diagram illustrating dialectic as one of the seven liberal arts. Philosophy is subdivided into grammar, rhetoric, dialectic, arithmetic, geometry, astronomy and music.

1. Introduction

Dante’s use of logic has been, with some rare exceptions, a quite neglected topic among scholars. Nonetheless, Dante’s logical competence was something well recognized by his early biographers and commentators, exactly as in the more famous case of his primo amico Guido Cavalcanti. The following are some illustrative cases:

G. Boccaccio, Trattatello in laude di Dante (1362): disputando, più volte mostrò l’altezza del suo ingegno, che ancora, narrandosi, se ne maravigliano gli uditori

Benvenuto da Imola, Comentum super Dantis Aldigherij Comoediam (1380): definitivo, divisivo, probante, rimprocacciante ed esempilificativo […] spesso appoggia con ragione ed argomenti i suoi detti [e] rimprovera e confuta i detti altrui

Leonardo Bruni, Vita di Dante (1436): un parlatore rado e tardo, ma nelle sue risposte molto sottile […] in molte canzoni sottile e limato e scientifico

In all these passages a terminology is deployed that clearly addresses Dante’s logical competence: “disputando” alludes to the art of logical disputation typical of the scholastic and university environments (Weijers 1995; 2013); “probante” remarks an expertise in building proofs and sound demonstrations; and “sottile e limato e scientifico” directly refers to the Aristotelian (and medieval) conception of “science” as a knowledge of causes grounded on syllogism (cf. Posterior Analytics I, 2; II 3–10). Additionally, it is worth noting that this sensitivity towards Dante’s use of logic continued also in the Italian Renaissance and in the anti-papal circles of the Protestant countries, where the Monarchia was first published and edited. Just to mention a couple of examples, the vernacular edition of Cicero’s Topica by Pompeo and Simone della Barba (1556) has an extremely relevant commentary, in which the Ciceronian loci are illustrated with examples drawn from Dante, Petrarca, and Boccaccio. And some early editions of the Monarchia, such as the princeps by Johannes Oporinus (1559) and German editions by Johannes Heroldt (1556) and Henri-Albert Gosse (1740) beautifully instantiate the reception of the logical language of the Monarchia, sometimes delving also into its technicalities. Thus, studying Dante’s logic today continues a long tradition of historical reception to which we can continue to add.

Vernacular edition of Cicero’s Topica translated by Simone della Barba (1556; first vulgarization: Florence, 1552) with commentary by his brother Pompeo della Barba. We also owe the Ciceronian “topics” to Pompeo, illustrated with examples from Dante, Petrarch and Boccaccio, and the translation of Boethius’ “Differenze locali”, added in appendix to the Ciceronian text almost as a compendium. The editor is Gabriele Giolito de Ferrari, in Venice (“Vinegia”). On the colophon we can admire his mark: a phoenix on flames that emanate from an amphora bearing the initials G.G.F. The amphora is supported by two winged satyrs. On the ribbon we read the motto “De la mia morte eterna vita i vivo”. – “Semper eadem”.

The editio princeps of Monarchia (K) was printed in reformed Basel in 1559 by Johannes Oporinus. This edition placed Dante’s treatise amongst other Latin treatises on imperial authority.

2. The truth that sets humanity free

In Convivio Book III Chapter xv, Dante, echoing Boethius, describes the demonstrations of philosophy – which is “gloriosa di libertade” – as the eyes of the mind that set us free from the restrictions of our ignorance:

Convivio II, xv 2: Ove si vuole sapere che questa donna è la Filosofia; la quale veramente è donna piena di dolcezza, ornata d’onestade, mirabile di savere, gloriosa di libertade […]. Li occhi di questa donna sono le sue dimostrazioni, le quali, dritte ne li occhi dello ’ntelletto, innamorano l’anima, liberata nelle [sue] condizioni. […] Ove si dice: ‘sed e’ non teme angoscia di sospiri’, qui si vuole intendere: s’elli non teme labore di studio e lite di dubitazioni, le quali dal principio delli sguardi di questa donna multiplicatamente surgono, e poi, continuando la sua luce, caggiono quasi come nebulette matutine alla faccia del sole; e rimane libero e pieno di certezza lo familiare intelletto, sì come l’aere da li raggi meridiani purgato e illustrato. (ed. Fioravanti 2014; emphasis added)

Here we must observe that this lady is Philosophy, who truly is a lady full of sweetness, adorned with honor, wondrous in wisdom, glorious in freedom […]. […] the eyes of this lady are her demonstrations, which when directed into the eyes of the intellect, enamor the soul that is liberated from its earthly condition. […] Where it is said Provided he fears not the sighs of anguish, we must understand provided he fears not the strain of study and the turmoil of uncertainty which spring forth in profusion from this lady’s first glances, and then, as her light continues, fall away like morning clouds before the face of the sun, so that the intellect becomes accustomed to her and remains free and full of certainty, like the air that is purged and made luminous by the midday rays. (Trans. Lansing 1990)

The very same idea of a liberation realized through the means of a scientific demonstration is also at the core of our political treatise (Tabarroni-Chiesa 2011; Chiesa 2018). As we know, in the first prologue Dante declares that his scientific task will be that of “intemptatas ab aliis ostendere veritates”, i.e. revealing truths never tried by others. Specifically, he seeks to determine the most useful and hidden one (“utilissima et maxime latens”), which is the exact truth about temporal monarchy (“temporalis monarchie notitia”):

Monarchia I, i 3-5: Hec igitur sepe mecum recogitans, ne de infossi talenti culpa quandoque redarguar, publice utilitati non modo turgescere, quinymo fructificare desidero, et intemptatas ab aliis ostendere veritates […]. Cumque, inter alias veritates occultas et utiles, temporalis Monarchie notitia utilissima sit et maxime latens et, propter non se habere inmediate ad lucrum, ab omnibus intemptata, in proposito est hanc de suis enucleare latibulis, tum ut utiliter mundo provigilem, tum etiam ut palmam tanti bravii primus in meam gloriam adipiscar.

Thinking often about these things, lest some day I be accused of burying my talent, I wish not just to put forth buds but to bear fruit for the benefit of all, and to reveal truths that have not been attempted by others […]. Now since among other truths which are hidden and useful, a knowledge of temporal monarchy is both extremely useful and most inaccessible, and since no one has attempted to elucidate it (on account of its not leading directly to material gain), I propose to draw it forth from where it lies hidden, so that my wakeful nights may be of benefit to the world, and so that I may be the first to win for my own glory the honour of so great a prize. (Trans. Shaw 1996)

In the second prologue, then, he completes these declarations by stating prophetically that this revelation will lead to a collective liberation of humanity from the chains of ignorance and the more concrete bonds of political servitude. Thanks to the strict necessity of his conclusions, the usurpers will understand that they are wrong and the subjects will understand that they are free from the usurpers’ yoke:

Monarchia II, i 5-6: Verum quia naturalis amor diuturnam esse derisionem non patitur, sed, ut sol estivus qui disiectis nebulis matutinis oriens luculenter irradiat, derisione omissa, lucem correctionis effundere mavult, ad dirumpendum vincula ignorantie regum atque principum talium, ad ostendendum genus humanum liberum a iugo ipsorum, cum Propheta sanctissimo me me subsequenter hortabor subsequentia subassummens: «Dirumpamus» videlicet «vincula eorum, et proiciamus a nobis iugum ipsorum» […]. Nam per hoc quod romanum Imperium de iure fuisse monstrabitur, non solum ab oculis regum et principum, qui gubernacula publica sibi usurpant, hoc ipsum de romano populo mendaciter extimantes, ignorantie nebula eluetur, sed mortales omnes esse se liberos a iugo sic usurpantium recognoscent.

But since natural love does not allow scorn to last long, preferring (like the summer sun which as it rises disperses the morning clouds and shines forth radiantly) to cast scorn aside and to pour forth the light of correction, I too then, in order to break the chains of ignorance of kings and princes such as these, and to show that the human race is free of their yoke, shall take heart along with the most holy prophet, by making my own the words of his which follow: ‘Let us burst their chains, and cast their yoke from us’ […] For showing that the Roman empire is founded on right will not only disperse the fog of ignorance from the eyes of kings and princes who usurp control of public affairs for themselves, falsely believing the Roman people to have done the same thing, but it will make all men understand that they are free of the yoke of usurpers of this kind.

From these passages, we come to understand the reason why Dante attributed such an important role to logic and its terminology in the Monarchia: the capability of the intemptatas veritates to induce this general liberation resides precisely in their irrefutability, i.e. in their logical cogency and necessity. In this way, Dante merges the biblical idea according to which the knowledge of the truth automatically produces a liberation (John 8:32, NIV: “Then you will know the truth, and the truth will set you free”) with the more recent image of logic as an art of arts (ars artium) necessary to avoid errors and achieve scientific certainty (Fioravanti 1992).

3. Dante’s ‘technical’ use of logic

3.1. Monarchia I, xi: Dante and the Syncategoremata

Reading the Monarchia, it is immediately evident that for Dante it is crucial to make explicit the logical underpinnings of both his refutations (i.e. when he has to shed a “lux correctionis”) and his “positive” arguments (i.e. when the goal is to “ostendere”). An emblematic example of a “positive” demonstration can be drawn from Book I, where Dante argues in favor of the necessity of the universal monarchy. In Chapter xi, he claims that only a universal monarch can be just in the highest degree and therefore ensure that the whole world is ruled according to justice in the highest degree. He begins his treatment of the issue with the following argument:

Monarchia I, xi 8:
(1) Iustitia potissima est in mundo quando volentissimo et potentissimo subiecto inest.
(2) Huiusmodi solus Monarcha est.
(⸫) Ergo soli Monarche insistens iustitia in mundo potissima est.

(1) Justice is at its strongest in the world when it resides in a subject who has in the highest degree possible the will and the power to act.
(2) Only the monarch is such a subject.
(⸫) Therefore, justice is at its strongest in the world when it is located in the monarch alone.

To this argument Dante adds a rather technical remark, introducing, just like Aristotle did in the Organon, the use of variables:

Monarchia I, xi 9: Iste prosillogismus currit per secundam figuram cum negatione intrinseca, et est similis huic: omne B est A; solum C est A: ergo solum C est B. Quod est: omne B est A; nullum preter C est A: ergo nullum preter C est B.

This prosyllogism is of the second figure with intrinsic negation, and it takes this form: all B is A; only C is A; therefore only C is B. That is: all B is A; nothing except C is A; therefore, nothing except C is B.

This passage represents very well the way in which logic is deployed in the Monarchia. In the first place, we find an exhibited deployment of a specialized language: the argument is presented as a “prosyllogism” (“prosyllogismus”), which technically means a secondary syllogism devoted to the demonstration of one of the premises of a primary or main syllogism. In this case, its conclusion coincides with the minor premise of the syllogism which he had presented at the beginning of the chapter:

Secondly, Dante displays his syllogism in a scheme through variables, telling us that it “runs through the second figure with an intrinsic negation” (“cum negatione intrinseca”):

If we recall that a “second figure” syllogism is a syllogism that has a negative premise and a negative conclusion, we immediately realize the originality of Dante’s solution. Instead of using traditional negative propositions (e.g. No A is B; Some A is not B), Dante uses a negation which remains implicit, being implied by the semantics of the terms ‘only’ (solum) and ‘nothing except’ (“nullum preter”). These were very special syncategorematic terms that medieval logicians used to call “dictiones exclusivae” (“exclusive words”) and “exceptivae” (“exceptive words”). In a later period, these dictiones were also named “exponibilia” (“exponible words”), from their property of concealing a hidden meaning further exponible and analyzable (cf. Maierù 1972; Mozzillo-Howell 1998). In this case, the term ‘solum’ carries out an intrinsic negation (negatio intrinseca), that is brought forth when it is shown to mean “nullum preter” (“no one except for”). Thus, Dante perfectly fulfills the formal requirements of a second figure syllogism: in fact, we can recognize a sort of modified “Camestres”, i.e. a syllogism of the form “All B is A; No C is A; No C is B” with the addition of the “except” (“preter”) clause. Without going into specifics, it is worth noting that these semantic notions were typically conveyed by the so-called treatises on Syncategoremata, i.e. works on grammatical terms endowed with specific logical properties. For instance, in Peter of Spain’ Syncategoremata the idea that exclusive words imported a negation was presented as follows:

Peter of Spain, Syncategoremata, VIII 57: […] Unde dico quod in dictionibus exclusivis per impositionem earum intelligitur negatio, quia ‘tantum’ et ‘solus’ ex sua impositione significant ‘non cum alio’.

Hence I say that in exclusive words one understands a negation in virtue of their imposition, for it is in virtue of their imposition that the word ‘only’ and ‘alone’ signify ‘not with another’ (Trans. Spruyt 1992)

And the properties of “solum” and “preter” were typically described in the following way:

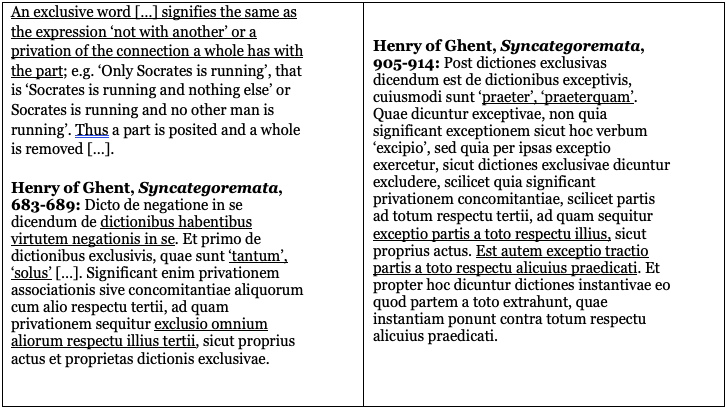
Strikingly, at the beginning of the 14th century, the rules of conversion concerning these terms were also gathered in the emerging treatises on consequences (consequentiae) (Mozzillo-Howell 1998; 2012). If we consider the early treatises edited by N.J. Green-Pedersen (1980; 1983), we find the statement of the following principles, according to which an affirmative exclusive proposition is equivalent to a negative exceptive one:

Anonymi de consequentiis (MS London, BL Royal 12 F XIX), 57: Ostendo quod haec consequentia est bona: ‘nihil praeter hominem est animal, ergo nihil praeter animal est homo’. Quia sequitur ‘nihil praeter hominem est animal, ergo tantum homo est anima’ […]; quia affirmativa exclusiva aequipollet exceptivae negativae in qua fit exceptio a trascendente.

William Burley, De consequentiis, 34: […] Quaelibet exclusiva habet duas exponentes; ut ista ‘tantum homo currit’ et ‘nihil aliud ab homine currit’.

Walter Burley, De consequentiis, 51: Et notandum quod ab exclusiva affirmativa ad exceptivam negativam in eisdem terminis tenet consequentia. Unde sequitur ‘tantum Socrates currit, ergo nihil praeter Socratem currit’.

MS London, British Library 6891, f. 3v: This is the passage of Monarchia I, xi 9 in which Dante uses the notion of “prosyllogism”, which technically means a secondary syllogism, devoted to the demonstration of one of the premises of a primary or main syllogism. In what follows we find the deployment of the terms ‘solum’ and “nullum preter”. Finally, in this segment we can easily recognize the use of letters as variables within the schematization of the syllogistic argument (lines 4-5). On the right margin of the folium we also find an index, or “manicule” (from the Latin word “manicula”, meaning “little hand”), that points to the importance of this portion of the text:

3.2. Monarchia III, viii: Dante and the ‘proprietas terminorum’

Another beautiful example of Dante’s knowledge of the Syncategoremata and of his tendency to formalize demonstrations can be taken from Book III Chapter viii. Here he translates the standard “papist” argument from Matthew 16 in a syllogistic form:

Monarchia III, viii 1-3: Item assummunt de lictera eiusdem illud Cristi ad Petrum: ‘Et quodcunque ligaveris super terram, erit ligatum et in celis; et quodcunque solveris super terram, erit solutum et in celis’ […] Sillogizant enim sic:

(1) Petrus potuit solvere omnia et ligare.

(2) Successor Petri potest quicquid Petrus potuit.

(⸫) Ergo successor Petri potest omnia solvere et ligare.

They likewise take from the text of Matthew those words of Christ to Peter: ‘And whatsoever thou shalt bind on earth shall be bound in heaven; and whatsoever thou shalt loose on earth shall be loosed on heaven’ […] Their syllogism takes this form:

(1) Peter could loose and bind all things.

(2) Peter’s successor can do anything Peter could do.

(⸫) Therefore, Peter’s successor can loose and bind all things.

As we know, the words from Matthew’s Gospel referring to Peter’s privilege of binding or loosing on Earth were particularly debated in the Middle Ages (cf. Lambertini 2011; Quaglioni 2015). Specifically, the meaning of the universal term “whatsoever” (“quodcunque”) was particularly controversial. Dante reshapes this issue in strictly logical terms, focusing on the range of reference (“distributio”) of the terms “all” (“omne”) and “whatsoever” (“quodcunque”). In particular, he focuses on what he considers the major premise of the syllogism, stating that he will not accept it without drawing a distinction (i.e. using a solutio distinctiva; cf. Barolini 2018). Displaying a technical terminology, Dante remarks that the universal sign “omne” , which is implied in “quodcunque”, is never distributed beyond the scope of the term to which it refers and so it is not to be taken in an absolute sense:

Monarchia III, viii 4-5: Minorem concedo, maiorem vero non sine distinctione. Et ideo dico quod hoc signum universale ‘omne’, quod includitur in ‘quodcunque’, nunquam distribuit extra ambitum termini distributi. Nam si dico ‘omne animal currit’, ‘omne’ distribuit pro omni eo quod sub genere animalis comprehenditur […]

I grant the minor premiss, but I do not grant the major premiss without drawing a distinction. And thus I say that this universal sign ‘all’, which is contained in ‘whatsoever’, never refers beyond the scope of the term to which it refers. For example, if I say ‘all animals run’, the word ‘all’ refers to every creature which is included within the class ‘animal’ […]

He then determines the actual scope of the term “quodcunque” by looking at the evangelical passage itself. From the first part of Jesus’ promise: “I will give unto thee the keys of the kingdom of heaven”, Dante deduces that Peter was made the doorkeeper of the kingdom of heaven. Therefore, accordingly, the scope of “quodcunque” should be narrowed down (“contrahitur in sua distributione”) only to those things that pertain to the office of the keys (“ab offitio clavium”), from which the temporal jurisdiction is excluded:

Monarchia III, viii 8-10: […] manifestum est quod non absolute summenda est illa distributio, sed respective ad aliquid […] Dicit enim Cristus Petro: ‘Tibi dabo claves regni celorum’, hoc est ‘Faciam te hostiarium regni celorum’ […] Et sic signum universale quod includitur in ‘quodcunque’ contrahitur in sua distributione ab offitio clavium regni celorum: et sic assummendo, vera est illa propositio; absolute vero non, ut patet.

[…] it is clear that the range of reference is to be taken not in an absolute sense but in relation to something. […] For Christ says to Peter: ‘I will give unto thee the keys of the kingdom of heaven’, that is ‘I shall make you gate-keeper of the kingdom of heaven’. […] And thus the universal sign which is contained in ‘whatsoever’ is limited in its reference by the office of the keys of the kingdom of heaven.

In this case, Dante’s explanation reveals strong ties with the sections of the summule devoted to the so-called “properties of terms” (proprietas terminorum), such as restrictions (De restrictionibus) and distributions (De distributionibus). For instance, in Peter of Spain’s Tractatus, we find the following rule, which strictly matches our passage:

Peter of Spain, Tractatus XI 6: De termino restricto talis datur regula: si signum universale adveniat termino restricto, non distribuit ipsum nisi pro his ad que restringitur. Ut cum dicitur ‘omnis homo albus currit’; quia ‘homo’ restringitur ad albos, non potest distribui nisi pro albis.

A rule like this is given about a restricted term: if a universal marker comes next to a restricted term, it does not distribute it, except for those to which it is restricted. Take ‘every white man is running’ for example: since ‘man’ is restricted to white men, it cannot be distributed except for white men. (Trans. Dinneen 1990)

This refutation, in conclusion, beautifully instantiates Anthony K. Cassell’s famous claim according to which the Monarchia constitutes an “oasis of logic amid the tumult” (Cassell 2004, p. 3).

MS London, British Library 6891, f.14r: Monarchia III, viii 4-6: This is the passage concerning the interpretation of ‘quodcumque’ in Matthew 16:9. Dante remarks that the universal sign ‘omne’, which is implied in ‘quodcumque’, is never distributed beyond the scope of the distributed term, and so it is not to be taken in an absolute sense: ‘Et ideo dico quod hoc signum universale ‘omne’, quod includitur in quodcumque’ numquam distribuit extra ambitum termini distribuiti’ (lines 2-3).

3.3. Dante and the language of the ‘consequentiae’

Another aspect of logic particularly exhibited by Dante across the Monarchia is his accurate knowledge of the medieval theory of consequences (consequentiae), a branch of logical analysis especially concerned with the study of entailment and inference (Dutilh Novaes 2016). Medieval authors used to include under the notion of “consequentia” both conditional sentences and arguments, developing a conceptual framework that progressively absorbed the traditional syllogistic into a broader unified theory (Boh 1982; Stump 1982; Archambault 2018). At the beginning of the 14th century, a few specialized treatises on this subject began to appear, gathering and systematizing a language that was already circulating and codified in the treatises of Syncategoremata and some specific sections of the summule (particularly, those about hypothetical proposition: Green-Pedersen 1980; 1983; 1984). The first hint of Dante’s acquaintance with this theory is provided by the fact that at the end of Book I he explicitly refers to the chain of preceding syllogisms as a concatenation of “consequences” (consequentiae):

Monarchia I, xv, 10: Quod si omnes consequentie superiores vere sunt, quod sunt, necesse est ad optime se habere humanum genus esse in mundo Monarcham, et per consequens Monarchiam ad bene esse mundi.

Now if all the above consequences are true – as they are – for mankind to be in its ideal state there must be a monarch in the world, and consequently the well-being of the world requires a monarchy.

Furthermore, the poet quotes with exceptional precision the technical rules of this theory as they were collected in the specialized treatises and probably declaimed during oral disputations. The first case is a passage from Book II Chapter v, in which we find the statement that “in every consequence, it is impossible to have an antecedent without a consequent”:

Monarchia II, v, 22: Et cum in omni consequentia inpossibile sit habere antecedens absque consequente, ut hominem sine animali, sicut patet construendo et destruendo, inpossibile est iuris finem querere sine iure, cum quelibet res ad proprium finem se habeat velut consequens ad antecedens: nam inpossibile est bonam valetudinem membrorum actingere sine sanitate.

And since in any relationship of consequentiality it is impossible to have the antecedent without the consequent, as for example one cannot have ‘man’ without ‘animal’ – as is clear if one affirms the first while denying the second – it is impossible to seek the purpose of right without right, since each and every thing is related to its own particular purpose as consequent is to antecedent; e.g. it is impossible to have a healthy condition of the limbs without having good health.

This represents the criterion of validity for a conditional sentence as it was found in logical texts from Boethius on. Its concise formulation, however, along with the explicit use of the term “consequentia” (instead of “conditionalis” / “hypothetica propositio”) seems to share some similarities in particular with Peter Abelard’s influential formulation in the Dialectica (ca. 1117-21), and the aforementioned De consequentiis treatises:

Peter Abelard, Dialectica, tract. 3, lib. 1, ‘Divisio locorum differentiarum’: Videntur autem due consecutionis necessitates: una quidem largior, cum videlicet id quod dicit antecedens non potest esse absque eo quod dicit consequens; altera vero strictior, cum scilicet non solum antecedens absque consequenti non potest esse verum, <sed etiam> ex se ipsum exigit; que quidem necessitas in propria consecutionis sententia consistit et veritatem tenet incommutabilem ut, cum dicitur: ‘si est homo, est animal’, ‘homo’ proprie ad ‘animal’ ‘ antecedit, cum ex <se> ipso ‘animal’ exigit. Cum enim in substantia hominis animal contineatur, cum ‘homine’ semper ‘animal’ attribui contingit.

Anonymi de consequentiis, MS London, BL Royal 12 F XIX, par. 6: Et in consequentia bona antecedens non potest esse verum sine consequente.

Anonymi de consequentiis, MS Paris, BN lat. 16130, par. 26: In consequentia simplici requiritur quod antecedens numquam potest esse verum nisi consequens sit verum

Walter Burley, De consequentiis, par. 9; 70: consequentia simplici ita est quod antecedens non potest esse verum sine consequente […]. Nec antecedens potest esse verum nisi consequens sit verum; ut ‘si homo est, animal est’

An even more convincing correspondence with the rules gathered by the treatises on consequences is provided by the passage that immediately follows Dante’s statement that “in every consequence, it is impossible to have an antecedent without a consequent”. Here Dante refers to a possible objection, according to which it is always possible to obtain a true conclusion from a false syllogism:

Monarchia II, v 23-24: Propter quod evidentissime patet quod finem iuris intendentem oportet cum iure gradi; nec valet instantia que de verbis Phylosophi “eubuliam” pertractantis elici solet. Dicit enim Phylosophus: ‘Sed et hoc falso sillogismo sortiri: quod quidem oportet sortiri; per quod autem non, sed falsum medium terminum esse’. Nam si ex falsis verum quodammodo concluditur, hoc est per accidens, in quantum illud verum importatur per voces illationis; per se enim verum nunquam sequitur ex falsis, signa tamen veri bene secuntur ex signis que sunt signa falsi.

From this it is quite apparent that one who seeks the purpose of right must seek it with right; nor is this invalidated by the objection which is customarily based on Aristotle’s words where he discusses ‘eubulia’. For Aristotle says: ‘Yet it is possible to attain even good by a false syllogism: to attain what one ought, but not by the right means, the middle term being false’. For if a true conclusion is in some way arrived at from false premises, this happens by accident, inasmuch as the truth is introduced in the words of the conclusion; for in itself truth never follows from false premises, but words expressing truth may well follow from words which express falsehood.

In this case too, the sequence mirrors a typical pattern of the consequentiae treatises, in which the Aristotelian idea that from the false can follow the true, but not vice-versa, was codified as a rule (cf. Prior Analytics II; also used in Convivio IV, ix 6; and see Mozzillo-Howell 1998):

Anonymi de consequentiis, MS London, BL Royal 12 F XIX, par. 12: […] Sciendum quod in omni consequentia bona si antecedens est verum, consequens est verum, quia ex verum non sequitur falsum. Sed non oportet quod si antecedens est falsum, quod consequens sit falsum, quia ex falso bene potest sequi verum, sicut patet per Aristotelem I. Priorum: ex falsis verum, ex veris nil nisi verum.

Walter Burley, De consequentiis, par. 9-10: Item: in consequentia simplici ita est quod antecedens non potest esse verum sine consequente […]. Nota quod ex falsis potest sequi verum, sed ex veris non sequitur nisi verum. Unde versus: ex falsis verum, ex veris nil nisi verum

However, it should be noted that this principle was also conveyed by the Auctoritates Aristotelis, certainly known and consulted by Dante (Robiglio 2015):

Auctoritates Aristotelis (quas compilauit Iohannes de Fonte), opus 34 (Priora analytica II), 18: Ex falso bene sequitur verum sed ex vero numquam sequitur falsum sed semper verum unde ex falso verum ex vero nil nisi verum.

A last case in which Dante seems to quote a technical rule from the theory of the consequentiae is the following passage from Book II Chapter x:

Monarchia II, x 9: Et nota quod argumentum sumptum a destructione consequentis, licet de sua forma per aliquem locum teneat, tamen vim suam per secundam figuram ostendit, si reducatur, sicut argumentum a positione antecedentis per primam.

And note that our argument, which is based on denying the consequent, although valid in its form by virtue of a certain topic, yet reveals its full force as a second figure syllogism, if it is then reduced to the first figure as an argument based on affirming the antecedent

In this context he claims that his argument, which is based on the “destruction of the consequent” (“destructio consequentis”): (i) holds by a certain “locus”; (ii) is capable of showing all its inferential force (“vis”) only if reduced to a second figure syllogism as an argument based on the “positing of the antecedent” (“positio antecedentis”). Focusing on the first point, it should be recalled that, according to a once-influential hypothesis, medieval theories of consequences would have emerged solely from the tradition of commentaries on Topics (Bird 1961; Stump 1982). Later studies, however, have convincingly shown that the Topics were not the main source for the emergence of 14th-century theories of consequences, highlighting more relevant ties with the traditions of the Syncategoremata, of the summule (the parts on hypothetical syllogism), and the commentaries on Prior Analytics (Green-Pedersen 1984; Read 2015; Dutilh Novaes 2016). This passage from Monarchia II, x, in my view, clearly demonstrates that the importance of the Topics for the development of the consequentiae should not be dismissed altogether: the fact that the argument is said to hold in virtue of a certain “locus” faithfully reflects the Aristotelian conception of a ‘topic’ as a pattern of (correct) inference used to “find” and validate an argument. Additionally, it is worth noting that this claim was also present in the same treatises on “syncategorematic” terms addressed as the main sources of 14th century treatises on consequences:

Peter of Spain, Syncategoremata, V 41: Oportet quod in loco a primo ad ultimum semper confirmentur consecutiones intermedie per aliquos locos intrinsecos vel extrinsecos vel medios

Furthermore, in an argument from the beginning to the end it is necessary that the intermediate inferences always be confirmed by certain intrinsecal, extrinsecal or intermediary topics.

Henry of Ghent, Syncategoremata, 1066-1076: Sexta regula talis est: quidquid sequitur ad consequens, sequitur ad antecedens, ut ‘Si homo est, animal est; sed si animal est, substantia est; ergo si homo est, substantia est. Et per hanc regulam constat locus a primo ad ultimum. Et est locus a primo ad ultimum, quando pluribus consequentiis continue positis, ita scilicet quod illud quod est consequens in una est antecedens in alia, et ultimum consequens denotatur sequi ad primum antecedens. Et notandum quod ille locus solum tenet, quando in consequentiis intermediis illud quod est consequens in una consequentia et antecedens in alia, per eandem naturam fit antecedens in posteriori et consequens in priori.

Ibid, 1179-1183: Unde bene sequitur ‘Si homo est asinus, homo est rudibile”, sed non sequitur “Si est rudibile, non est risibile, quia illud repug<n>at homini, quia datur pro regula quod, quando antecedens est impossibile, numquam in consequentiis sequentibus tenet locus ab oppositis.

Ibid, 1096-1100: Et sic non tenet prima consequentia, immo consequens implicat contradictionem antecedentis; et sic tenet consequentia secunda, per locum ab oppositis. Vel potest dicere negationem simpliciter sive extra genus; tunc non ponit de se aliquod tempus, et sic bene tenet consequentia prima per locum a toto in quantitate.

Both Ockham and Burley, then, deploy this topical framework in their works on consequentiae: Burley explicitly claims that all valid consequences are based on dialectical topics (cf. Mozzillo-Howell 1998); Ockham incorporates in his theory the notions of “intrinsic” and “extrinsic” medium (cf. Green-Pedersen 1984). According to his Summa logicae (first years of the 1320s), a consequence holds in virtue of an intrinsic medium when it holds in virtue of the truth of a different sentence formed from its terms. For example, “Socrates is not running, therefore a man is not running” holds in virtue of this “intrinsic” medium: “Socrates is a man”, since if “Socrates is a man” is not true, the consequence does not hold. An “extrinsic” medium, by contrast, is a sentence not containing the terms that form the antecedent and the consequent of the consequentia, but which is a general rule describing the “fact” that warrants the passage from the antecedent to the consequent, and which concerns the form of sentences (cf. Dutilh Novaes 2016). Ockham’s example of a consequence holding in virtue of an “extrinsic” medium is “Only a man is a donkey, therefore every donkey is a man”, which holds in virtue of this general rule: “an exclusive and a universal with transposed terms signify the same and are convertible”.

Walter Burley, Tractatus longior, par. 117: Dico quod omnis consequentia bona tenet per aliquem locum logicum, non tamen oportet quod omnis consequentia bona tenet per aliquem locum dialecticum, nisi estendo dialecticam ad totam logicam

William of Ockham, Summa logicae, III III 1: Alia distinctio est quod aliquando consequentia tenet per medium extrinsecum, aliquando per medium intrinsecum. Et si dicatur contra istam distinctionem quod ista consequentia ‘Sortes non currit, ergo homo non currit’ tenet per istud medium extrinsecum ‘a singulari ad indefinitam postposita negatione est bona consequentia’, quod est medium extrinsecum: Dicendum est quod tenet per istud medium extrinsecum remote et mediate et insufficienter, quia praeter istam regulam generalem requiritur plus, scilicet quod Sortes sit homo; et ideo magis immediate et magis sufficienter tenet per istud medium ‘Sortes est homo’, quod est medium intrinsecum.

With reference to these passages, therefore, I propose to rehabilitate Bird and Stump’s hypothesis with this amendment: the Topics effectively exerted a key influence in the development of 14th century treatises on consequences, but almost always in a mediated way, i.e. through the material filter of broadly studied and diffused works such as the summule and the Syncategoremata. Even if the current availability of texts still does not allow for definitive conclusions, I find this picture – following the observations of Green-Pedersen (1984) – very plausible.

Finally, Dante’s quotation in Monarchia II, ix of the inferential patterns of positio antecedentis and destructio consequentis, along with the reducibility of consequences to syllogisms, deserves a couple of comments. Firstly, both the inferential patterns had already been codified in the summule and the Syncategoremata:

Consequentia P → Q antecedens → consequens

‘If Socrates is a man (P), then Socrates is an animal’ (Q)

Positio antecedentis P → Q, P ˫ Q

Destructio consequentis P → Q, not-Q ˫ not-P

Peter of Spain, Syncategoremata, V 34: Tertia regula talis est: ‘si aliquid sequitur ad aliud, destructo consequente destruitur et antecendens’. Et ob hoc semper tenet argumentum a destructione consequentis, ut ‘si est homo, est animal; ergo si non est animal, non est homo’. Quarta regula est talis: ‘si aliquid sequitur ad aliud, posito antecedente ponitur consequens’. Ut ‘si homo est, animal est; sed homo est; ergo animal est’. Et ob hoc tenet argumentum a positione antecedentis.

The third rule is the following: ‘If something follows from something else, then if the consequent is destroyed, so it is the antecedent’. That is why an argument from the destruction of the consequent is always sound, e.g. ‘If there is a man, there is an animal; therefore, if there is not an animal, there is not a man’. The fourth rule is the following: ‘If something follows from something else, then if the antecedent is asserted, so it is the consequent’. For example, ‘If there is a man, there is an animal; now there is a man; therefore, there is an animal’. That is why an argument from the assertion of the antecedent is sound.

Henry of Ghent, Syncategoremata, 1057-1062: Tertia regula est: si aliquid sequitur <ad> aliud, destructo consequente destruitur antecedens, ut “Si homo est, animal est; ergo si non animal est, non homo est”. Quarta regula talis est: si aliquid sequitur ad aliud, posito antecedente ponitur consequens, ut “Si homo est, animal <est>; sed homo est; ergo animal est”.

The inferential rule of the “detructio consequentis”, notably, is also used by Dante in Paradiso II and Convivio IV. In both cases he formulates a consequentia with the consequent bipartite in a disjunction, which is a specificity that we find in Monarchia III ii; xiv and Questio X as well. In Paradiso II this logical form is deployed by Beatrice to refute Averroes’ position (and Dante’s own in the Convivio) about the causes of the “dark spots” the surface of the moon; in Convivio IV, xii to disprove the idea that desire is a cause of “viltade”:

Dante, Paradiso II, 73-90:
Ancor, se raro fosse di quel bruno
cagion che tu dimandi (P), o d’oltre in parte
fora di sua materia sì digiuno
esto pianeto (Q), o, sì come comparte
lo grasso e ‘l magro un corpo, così questo
nel suo volume cangerebbe carte (R)
Se ‘l primo fosse, fora manifesto
ne l’eclissi del sol, per trasparere
lo lume come in altro raro ingesto
Questo non è (¬ Q): però è da vedere
de l’altro; e s’elli avvien ch’io l’altro cassi,
falsificato fia lo tuo parere. (…) (¬ R)

Convivio IV, xii 11-12: Veramente qui surge in dubio una questione, da non trapassare sanza farla e rispondere a quella. Potrebbe dire alcuno calunniatore della veritade che se per crescere desiderio acquistando, le ricchezze sono imperfette e però vili (P), che per questa ragione sia imperfetta e vile la scienza (Q), nell’acquisto della quale sempre cresce lo desiderio di quella […]. Ma non è vero che la scienza sia vile per imperfezione (¬ Q): dunque, per la distruzione del consequente, lo crescere desiderio non è cagione di viltade alle ricchezze (¬ P).

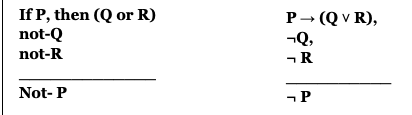
The idea according to which a consequentia can always be reduced to its syllogistic counterpart, on the other hand, seems instead to be a mature innovation of 14th-century theories of the consequences (cf. Mozzillo-Howell 1998):

Walter Burley, Tractatus longior, par. 117: Alia regula est ista: omnis consequentia bona habet reduci in syllogismum.

Remarkably, Dante specifies that this kind of reduction is somehow necessary to fully explicate the inferential force (the “vis”) of his argument. This, in our view, probably means: (i) that Dante still considered the syllogism as a privileged form of demonstration; (ii) that, in any case, he was aware that the advanced tools he was using still needed a translation into syllogistic terms to be better accepted and recognized as valid by everyone (Chiesa-Tabarroni 2013). This extraordinary passage, in other words, seems to suggest that Dante had a more nuanced and cutting-edge understanding of logic than many of his readers and contemporaries.

MS London, British Library 6891, f. 13r:Monarchia III, v: In this excerpt, we note again an instance of schematization with variables (lines 9-10). Additionally, we find the quotation of the technical rule from the theory of the consequences according to which ‘pro antecedente bene infertur antecedens’ (line 11), and of the fallacy ‘not-cause as a cause’ (non causam ut causam; final line).

4.Dante’s ‘poietic’ use of logic

Dante uses the language of the syllogism, in its practical version, at least three times in his treatise to create metaphors and similes. I would like to call it a “poietic” use of logic, availing of the original sense of the Greek term ποιητικός (poietikòs), i.e. “creative”, “productive”, “formative”. In all these cases, logical notions are creatively deployed by the craftsman Dante to speak directly about things without entering the mode of rational demonstration.

The first locus is in Book I, Chapter xv, where the structure of the syllogism is used to describe the relationship between the universal Emperor and the princes subordinated to him. Specifically, the local princes should receive from the Emperor common laws as major premises of a syllogism, to be integrated with particular premises accordingly to specific situations:

Monarchia I, xiv 7: Quam quidem regulam sive legem particulares principes ab eo recipere debent, tanquam intellectus practicus ad conclusionem operativam recipit maiorem propositionem ab intellectu speculativo, et sub illa particularem, que proprie sua est, assummit et particulariter ad operationem concludit.

This rule or law should be received from him by individual rulers, just as the practical intellect, in order to proceed to action, receives the major premiss from the theoretical intellect, and then derives the minor premise appropriate to its own particular case, and then proceeds to the action in question.

The resulting simile can be schematized as follows:

The second locus is in Book II, Chapter vi, when Dante claims that the human end represents the middle term of the universal end of nature. In this case, the simile gives way to a much stronger assertion: the human end properly is a necessary middle term (“aliquod medium necessarium”) for the achievement of the universal end of the Nature. Logic, in this way, seems to be directly assimilated to the ultimate language in which the “great book of Nature” – to quote Galilei – has been written by God the Creator:

Monarchia II, vi 5: Cum ergo finis humani generis sit aliquod medium necessarium ad finem nature universalem, necesse est naturam ipsum intendere.

Since therefore the goal of humanity is itself a necessary means to achieving the universal goal of the nature, it is necessary that nature wills it.

Finally, the third locus is in Book III, Chapter xvi, when the two types of happiness (“beatitudines”) are compared to two different conclusions, which must be reached through different middle terms: the first through the philosophical teachings (“per phylosophica documenta”), and the second through spiritual teachings (“per documenta spiritualia”):

Monarchia III, xvi 7-8: Duos igitur fines providentia illa inenarrabilis homini proposuit intendendos: beatitudinem scilicet huius vite, que in operatione proprie virtutis consistit et per terrestrem paradisum figuratur; et beatitudinem vite ecterne, que consistit in fruitione divini aspectus ad quam propria virtus ascendere non potest, nisi lumine divino adiuta, que per paradisum celestem intelligi datur.

Ad has quidem beatitudines, velut ad diversas conclusiones, per diversa media venire oportet. Nam ad primam per phylosophica documenta venimus, dummodo illa sequamur secundum virtutes morales et intellectuales operando; ad secundam vero per documenta spiritualia que humanam rationem transcendunt, dummodo illa sequamur secundum virtutes theologicas operando, fidem scilicet, spem et karitatem.

Ineffable providence has thus set before us two goals to aim at: i.e. happiness in this life, which consists in the exercise of our own powers and is figured in the earthly paradise; and happiness in the eternal life, which consists in the enjoyment of the vision of God (to which our own powers cannot raise us except with the help of God’s light) and which is signified by the heavenly paradise. Now these two kinds of happiness must be reached by different means, as representing different ends. For we attain the first through the teachings of philosophy, provided that we follow them putting into practice the moral and intellectual virtues; whereas we attain the second through spiritual teachings which transcend human reason, provided that we follow them putting into practice the theological virtues, i.e. faith, hope and charity.

5. Dante’s ‘exhibited’ use of logic and the creation of an authorship

This brings us to our final point and conclusions. Why do we find such an “exhibited” use of logic in a political work like the Monarchia? We have already seen how Dante in the Prologues insists on his scientific task of “ostendere veritates” and on the idea that this operation is intended to induce – through irrefutable demonstrations – a general liberation of humanity. In our view, however, there is yet another reason, which is Dante’s creation, across the treatise, of a specific kind of authorship. From the opening words of the first Prologue to the closing exhortation of the last chapter, the Poet strives to present himself as a qualified scientist-prophet assigned to the task of revealing a truth that exceeds the limitations of historical contingency – being valid in any time and any place. From this viewpoint, the atemporal and universal validity of logic – to which even St. Francis in the episode of Inferno 27 must bow – constitutes the methodological guarantee that the scientific conclusions reached by the treatise ultimately coincide with God’s own conclusions, representing the cornerstone of their intrinsic freeing power. As Chiesa and Tabarroni noted:

Nuova è l’idea che il metodo sillogistico—quello che poggia sulla logica, che non si contraddice, e come tale porta l’uomo a conclusioni che sono le conclusoni di Dio—sia la forma giusta per presentarli e discuterli, perché la correttezza del ragionamento diviene inconfutabile garanzia della validità dei risultati. (Chiesa-Tabarroni ed., CXLII)

What is new is the idea that the syllogistic method—a method that relies on logic, that does not contradict itself, and that, therefore, leads us to conclusions that are God’s conclusions—is the right format in which to present and discuss these theses, because the correctness of the reasoning becomes an irrefutable guarantee of the validity of the conclusions. (Trans. Barolini 2018)

The exhibition of a logical expertise, thus, represents a conditio sine qua non for the success of the mission of the treatise as well as for the “worthiness of faith and obedience” (cf. Convivio IV, vi 5) of his author. As Teodolinda Barolini brilliantly remarked, however, the irrefutability of the “intemptatae veritates” in their convergence with the Scriptures does not prevent Dante from creating space for difference and divergence even within the unwavering unity and convergence of the absolute Truth – thus creating an indissoluble link with one of the major themes of the Paradiso:

Barolini, “Dante squares the circle,” p. 56: Who then was Dante? Was he the single-minded possessor of absolute truth, donning his breastplate for battle, or was he the flexible inventor, through solutio distinctiva, of his very own doctrine of a double, or indeed multiple, truth, like the multiple and apparently contradictory viewpoints that are reconciled in the divine circles of the heaven of the sun? He was both, and both stances are present in both Paradiso and Monarchia.

Understanding why Dante takes the role of a logically expert truth-teller, finally, requires taking into account some fundamental ‘contextual’ reasons.

It should be first considered that Dante’s major opponents were, as Cassell noted, “towering experts in the field of logic” (e.g. Giles of Rome, James of Viterbo, Matthew of Acquasparta, Augustinus Triumphus of Ancona). Therefore, it is realistic to think that the poet felt the need to expose their “regnar per forza e per sofismi” (Paradiso XI, 5) through a commensurate deployment of technical tools. Anthony K. Cassell wrote (2004):

Cassell, The Monarchia Controversy, p. 31: He is fully aware that major defenders of hierocracy have been and still are, towering experts in the field of logic. Facing such odds he strides into the wrestling ring for the championship.

Secondly, Dante seems to deliberately distance himself from two different professional categories of his time. On the one side, the decretalisti, papist legisti who dealt with politics but sine arte, i.e. without using reason and method. Dante refers to them several times in the course of his works, as in Paradiso IX; Paradiso XII; and in Epistola XI. In Monarchia Book III, Dante drives them out of the arena because they are said to be completely devoid of any philosophical and theological competence:

Monarchia III, iii 9: Sunt etiam tertii – quos decretalistas vocant – qui, theologie ac phylosophie cuiuslibet inscii et expertes, suis decretalibus quas profecto venerandas existimo – tota intentione innixi, de illarum prevalentia – credo – sperantes, Imperio derogant.

There is also a third category, called decretalists – ignorant and lacking in any philosophical or theological training – who argue their case exclusively with reference to their decretals (which I certainly think worthy of veneration); trusting in their authoritativeness, I believe, they disparage the Empire.

The lack of demonstrative method typical of the decretalisti was something widely criticized by the theologians of Dante’s time, as well as by the philosophers (Maccarrone 1955). If we take the Principium in loica by Gentile da Cingoli (ca. 1295), which is an inaugural sermon held at the beginning of a course in logic in Bologna, we read that it is not possible to learn any science without the aid of logic, because otherwise, science turns into a “fabulatio” (“fabulation”). The “legisti,” from this point of view, are doubly failures, in their proceeding ‘historically’ (“ystorialiter”) and in their proceeding without logic (“sine loica”):

Gentile da Cingoli, Principium in loyca probissimi viri magistri Gentili, MS Palermo, Biblioteca Comunale, 2.Qq. D.142, f. 813; ed. Fioravanti 1992): Non potest addisci scientia aliqua sine loyca nisi fabulative […] Sed dubium est de istis legistis, quia vedientur esse sine loyca, eo quod ystorialiter procedunt […]. Legiste sunt servi dupliciter, primo modo quia obediunt legibus, sicut nos, secundo quia obediunt libris.

The incipit of Gentile’s Flores gramatice, preserved in Columbia University Library, MS Plimpton 139

In my view, it is highly likely that Dante wanted to mark – through logic – his distance from the legisti, using a language that is “with logic” — cum loica — and proper of a true philosopher-theologian. Alongside this methodological opposition, there is yet another critique in the Monarchia that is even more subtle and implicit. If we take Book I, Chapter xii, we find the sole passage in which Dante refers explicitly to logicians. Besides finding a hint of his consultation of some written logicalia (i.e. logical textbooks), we learn that “our logicians” (“logici nostri”), in their examples, are far from the meanings of the words they use – just like those who quote the definition of free will without having a correct understanding of it:

Monarchia I, xii 2: Veniunt namque usque ad hoc: ut dicant liberum arbitrium esse liberum de voluntate iudicium. Et verum dicunt; sed importatum per verba longe est ab eis, quemadmodum tota die logici nostri faciunt de quibusdam propositionibus, que ad exemplum logicalibus interseruntur; puta de hac: ‘triangulus habet tres duobus rectis equales’.

For they go so far as to say that free will is free judgment in matters of volition. And what they say is true, but they are very far from understanding what the words mean, just like our logicians who daily enunciate certain propositions by way of example in their discussions on logic, such as ‘a triangle has three angles equal to two right angles’.

Dante’s art of drawing distinctions (cf. Barolini 2018) is pointing out the possibility of bad use of logic, which was probably widespread in certain academic and institutional environments of his time. In a lecture in praise of Grammar pronounced by an anonymous master in Bologna at the very beginning of the 14th century, we find an extraordinary passage (cf. Fioravanti 1992). Philosophy is described as the mulier amicta sole of Apoc. 12:1: whereas the crown made of twelve stars represents the 12 Books of the Metaphysics, the moon under her feet represents logic. It is then stated that when it is far from the sun (i.e. true philosophy) it is less bright than when it is joined to it. In other words, the more distant logic is from philosophy, the more obscure it becomes:

Sermo ‘Accipe igitur haustum’, MS Sevilla, Biblioteca Capitular y Columbina, 81.6.66, ff. 85r-87v; ed. Fioravanti 1992: Ratio autem quare per lunam intellegitur loyca hec est, quia ut dicit Martinianus, quando luna distat a sole minus illuminatur quam quando est cum sole coniuncta, quia tunc illuminatur a parte superiori et quia propinquior est soli plus recipit de lumine. Sic est loica, tunc distat a sole quando non est unita cum philosophia.

This accusation, this duplicity, is very close to the one that we find in the Monarchia, and could possibly be seen as a reaction to the same historical phenomenon: a hypertrophic growth of logic at an institutional level and its claim for the status of an independent discipline (cf. Fioravanti 1992).

References:

Alighieri, Dante. Monarchia. Opere minori, III, 1, Bruno Nardi (ed.). Milano-Napoli: Ricciardi, 1979.

________. Monarchy, Prue Shaw (ed.). Cambridge: Cambridge University Press, 1996.

________. Monarchia, Paolo Chiesa and Andrea Tabarroni (eds.). Roma: Salerno Editrice, 2013.

________. Monarchia, Diego Quaglioni (ed.). Milano: Mondadori, 2015.

Archambault, Jacob. ‘Introduction: Consequences in Medieval Logic’. Vivarium 56 (3-4) (2018), 201-221.

Barolini, Teodolinda. ‘Dante Squares the Circle: Textual and Philosophical Affinities of Monarchia and Paradiso (Solutio Distinctiva in Mon. 3.4.17 and Par. 4.94-114)’. Dante as Political Theorist: Reading Monarchia, ed Maria Luisa Ardizzone. Cambridge Scholars Publishing, 2018, 33-59.

Bird, Otto. ‘Topic and consequence in Ockham’s logic’. Notre Dame Journal of Formal Logic 2, (1961), 65-78.

Boh, Ivan. ‘Consequences’. The Cambridge History of Later Medieval Philosophy, Norman Kretzmann, Anthony Kenny, and Jan Pinborg (eds.). Cambridge: Cambridge University Press, 1982, 300–314.

Cassell, Anthony. The Monarchia Controversy: An historical study with accompanying translations of Dante Alighieri’s Monarchia, Guido Vernani’s Refutation of the Monarchia composed by Dante and Pope John XXII’s bull, Si fratrum. Washington, D.C.: Catholic University of America Press, 2004.

Chiesa, Paolo and Andrea Tabarroni. ‘Dante demonstrator nel secondo libro della ‘Monarchia’. Leggere Dante oggi. I testi, l’esegesi, Enrico Malato and Andrea Mazzucchi (eds.). Roma: Salerno Editrice, 2012, 141-162.

Chiesa, Paolo. ‘Dante ‘the Scientist’ and Dante the Prophet in the Three Prologues of Monarchia’. Dante as Political Theorist: Reading Monarchia, 2018, pp. 82-97.

Dutilh Novaes, Catarina. ‘Medieval Theories of Consequence’. The Stanford Encyclopedia of Philosophy (Fall 2016 Edition), Edward N. Zalta (ed.). <https://plato.stanford.edu/archives/fall2016/entries/consequence-medieval/>

Fioravanti, Gianfranco. ‘Sermones in lode della filosofia e della logica a Bologna nella prima metà del XIV secolo’. L’insegnamento della logica a Bologna nel XIV secolo, Dino Buzzetti, Maurizio Ferriani and Tabarroni (eds.). Bologna: Istituto per la Storia dell’Università, 1992, 165-185.

Green-Pedersen, Niels Jørgen. ‘Walter Burley, De consequentiis and the origin of the theory of consequence’. English Logic and Semantics, Henk A.G. Braakhuis, C.H. Kneepkens, Lambert M. De Rijk (eds.). Nijmegen: Ingenium, 1981, 279-201.

________. ‘Early British Treatises on Consequences’. The Rise of British Logic, Papers in Medieval Studies 7, Patrick Osmund Lewry (ed.). Toronto: Pontifical Institute of Medieval Studies, 1983, 285-307.

________. The Tradition of the Topics in the Middle Ages. Munich: Philosophia Verlag, 1984.

Lambertini, Roberto. ‘Logic, Language and Medieval Political Thought’. Logic and Language in the Middle Ages, Jakob Fink, Heine Hansen and Ana Maria Mora-Marquez (eds.). Leiden, The Netherlands: Brill, 2011, 419-432.

Maccarrone, Michele. ‘Il terzo libro della Monarchia’. Studi Danteschi 33 (1955), 5-142.

Maierù, Alfonso. Terminologia logica della tarda scolastica. Roma: Edizioni dell’Ateneo Roma, 1972.

Mozzillo-Howell, Elizabeth Marilyn. Dante’s Art of Reason: A Study of Medieval Logic and Semantics in the ‘Monarchy. Dissertation, Harvard University, 1998.

________. ‘Monarchia II. X and the medieval theory of consequences’. Italian Studies 57:1 (2002), 20-36.

Read, Stephen. ‘The medieval theory of consequence’. Synthese 187(3) (2015), 899–912.

Robiglio, Andrea. ‘Dante e le ‘Auctoritates Aristotelis’. Les Auctoritates Aristotelis, leur utilisation et leur influence chez les auteurs médiévaux. État de la question 40 ans après la publication, Vol. 83. Barcelona-Madrid: Fédération internationale des Instituts d’études médiévales (FIDEM), 2015, 187-202.

Stump, Eleonore. ‘Topics: their development and absorption into consequences’. The Cambridge History of Later Medieval Philosophy, Norman Kretzmann, Anthony Kenny, and Jan Pinborg (eds.). Cambridge: Cambridge University Press, 1982, pp. 273–299.

Weijers, Olga. La ‘disputatio’ à la Faculté des arts de Paris (1200-1350 environ). Turnhout: Brepols, 1995.

________. In Search of the Truth. A History of Disputation Techniques from Antiquity to Early Modern Times. Turnhout: Brepols, 2013.

Recommended Citation: Pelizzari, Stefano. “‘Intemptatas ab aliis ostendere veritates. Dante’s use of logic in the Monarchia.’” Digital Dante. New York, NY: Columbia University Libraries, 2020. <https://digitaldante.columbia.edu/pelizzari-logic/>