(For an introduction to my project diagramming astronomy in the Commedia, including introductory diagrams, see here.)
Inferno 1.37-40
The verses which, already in Inferno 1, open the poem’s episodic discourse on creation also constitute the first astronomical reference of the Commedia.
Temp’ era dal principio del mattino,
e ’l sol montava ’n sù con quelle stelle
ch’eran con lui quando l’amor divino
mosse di prima quelle cose belle
(Inf. 1.37-40)
As will frequently be the case throughout the Inferno, this reference to the stars appears to be an indication of the time, in this case both the time of day and the time of year.
It is the morning, “[t]emp’ era dal principio del mattino,” as the sun is just rising over the horizon, “e ’l sol montava ’n sù.” As we might expect, the essential spatiotemporality of the stars is focalized as the sun’s location correlates to a particular time of day. This essential and intuitive association between the stars and time, however, remains open to a number of interpretations. Minimally, the movement of the stars through space could be no more than a fixed correlation, signs of the times which change independently of celestial movement. Maximally, the movements of the stars could be causal, in other words the movement of the stars could be time itself. Put differently, in the former case the relationship between the stars and time is accidental, while in the latter case it is essential. Ancient and medieval theories about time and the cosmos fall somewhere along the axis that exists between these two extreme positions. In this opening passage of the Commedia, Dante provides us no indication of causality or determinism (neither temporal nor fatalistic), nor any information which might suggest one interpretation over another. All we find in these verses is a simple, normative observation: the cyclical movements of heavenly objects through space is tied to the experience of time upon the earth. We know that it is morning because we see the sun is rising, though the text presents the information in the opposite order: we are told it is the morning, and subsequently find that the sun is set presently to rise.
In this first astronomical periphrasis, Dante ties the onset of the pilgrim’s voyage—an event that is tantamount to the creation of the poet’s imagined world—to the creation of the putatively real world that exists outside the poetry. The sun is said to be rising with those same stars that accompanied it (the “lui” of verse 39 refers back to the “sole” of verse 38) when divine love (i.e., God) first “moved the things of beauty,” which is to say “created the world.” To set the world in motion is, given the Aristotelian aegis under which Dante so often locates himself, to create it. Accordingly, the sun has returned, as it would each year, to the place where its movement first began on the day of creation. A clear delineation of this place is suppressed in the text: nothing about Inferno 1 indicates beyond any shadow of doubt which set of stars the poet here references.
The critical consensus is, and has always been, that “quelle stelle” is a reference to the sign of Aries, the 30-degree segment of the ecliptic which immediately follows the location of the vernal equinox. (I will not argue against this consensus, but will offer some contextualizing comments about the fictive date of the journey at the end of this section on the stars of Inferno.) By stipulating Aries and the vernal equinox as the beginning of the annual cycle, Dante recalls a theological tradition which traces back to Philo of Alexandria’s Questions on Exodus, one which was codified at the First Council of Nicaea and further solidified in the work of the Venerable Bede in The Reckoning of Time (see Philo, Questions on Exodus. trans. Ralph Marcus, Harvard University Press, 1953. sec. 1.1, pp. 2-6; see also Bede, The Reckoning of Time. trans. Faith Wallis, Liverpool University Press, 1999. pp. 24-25). This association of creation with spring explicitly breaks with the astrological tradition, according to which the beginning of the annual cycle is located in midsummer (see, for example, Maternus, Firmicus, Matheseos Libri VIII. (Ancient Astrology Theory and Practice). trans. Jean Rhys Brahm, Noyes Press, 1975. sec. 3.1.9; p. 72; and Macrobius, Ambrosius Aurelius Theodosius, Commentary on the Dream of Scipio. trans. William Harris Stahl, Columbia University Press, 1990. p. 179). For further analysis of these cultural distinctions regarding the start to the yearly cycle, see the second chapter of my dissertation.
Dante is vague regarding the specific location of the sun within the 30-degree belt of Aries, and there is some disparity even within the theological tradition. Philo mentions the vernal equinox specifically: “(Scripture) thinks it proper to reckon the cycle of months from the vernal equinox. Moreover (this month) is said to be the ‘first’ and the ‘beginning;’ […].” While Bede postpones the creation of the sun to the fourth degree of Aries (approximately four days after the vernal equinox): “[t]hat is, [the sun], when it first rose above the Earth, was positioned in that part of the sky which philosophers call the fourth degree of Aries.” Bede’s notion that the sun was created at the fourth degree of Aries responds to a polemic regarding the account of the hexameron in Genesis, according to which light and dark—and day and night—existed as of the first day of creation, while the sun did not come into being until the fourth. To maintain the order of things, Bede posits that the sun was created at the fourth degree of Aries, in accord with its creation on the fourth day of worldly time. Dante does not wade into the specifics of this polemic in Inferno 1.
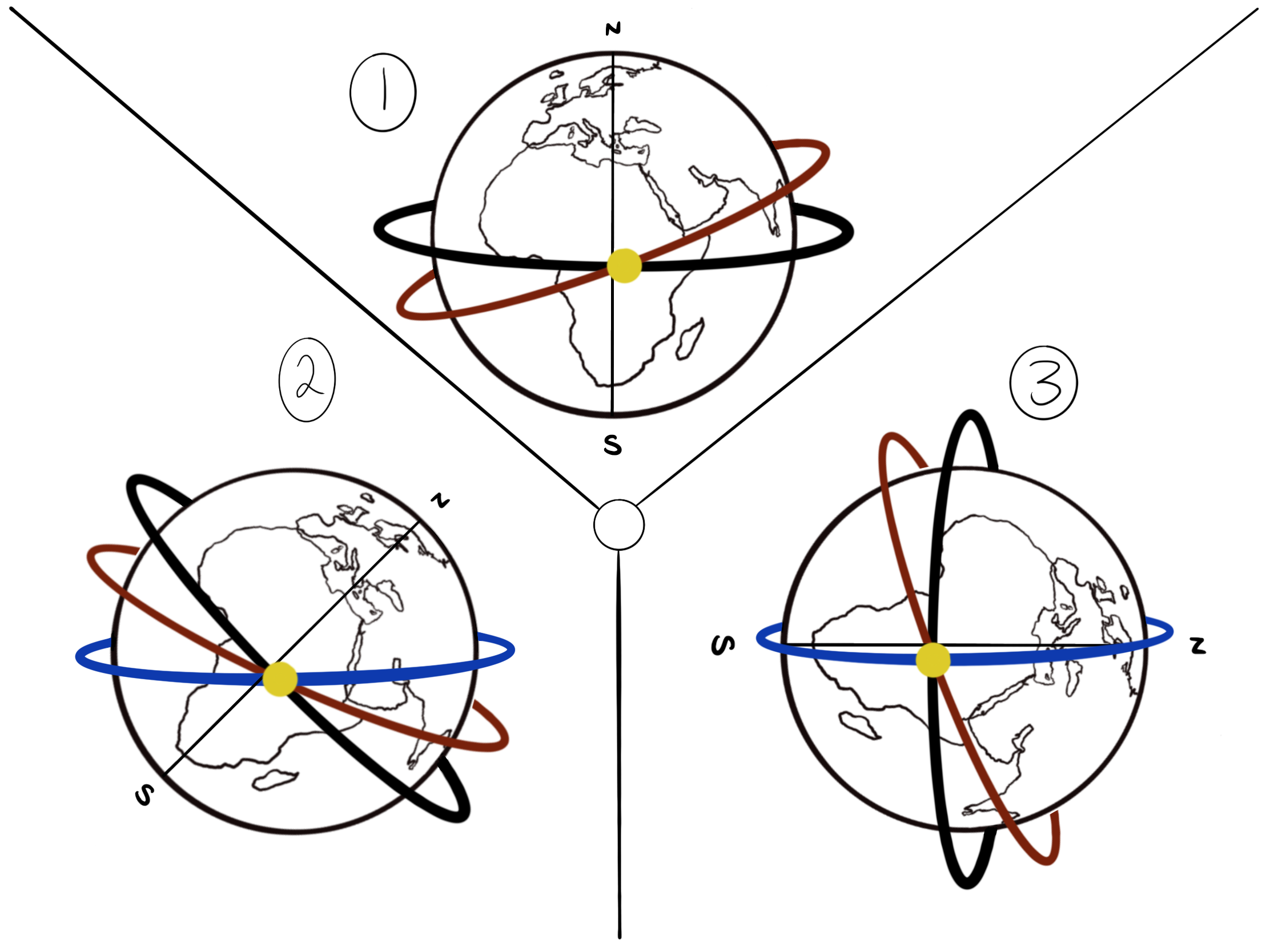
This opening shot of the skies also introduces the notion of a horizon line, which will grow in relevance as the pilgrim enters the southern hemisphere at the end of Inferno 34. The horizon is an optical phenomenon caused by the earth’s sphericity, meaning that it is determined by an observer’s relative position on the surface of the earth. We can imagine the horizon as a plane that emanates from the midpoint of the earth and is perpendicular to the imaginary axis that falls from the zenith, or highest point in the sky, down to the center of the earth, intersecting the given observational locus. Here are a few examples to illustrate how the horizon changes as the observational locus changes:
1) When standing on the north pole of the earth, the zenith will be marked by the north star, Polaris, or the north celestial pole; in this case, the line of the horizon is superimposed upon the equator, or the midpoint between the two poles. See diagram 1, where the perspective is that of an observer located at the north pole. Here, the black line is both the equator and the horizon, while the red line is the ecliptic.
2) When standing somewhere in between the northern pole and the equator, the zenith will be located at the highest point directly overhead the observer. The horizon is located on the plane which is perpendicular to the zenith at this location, and will necessarily be found between the two horizons denoted by P = north pole and P = equator. See diagram 2, where the perspective is that of an observer located in the northern hemisphere, at an arbitrary latitude south of the north pole and north of the equator of the earth. Here, the black line is the equator, the red line the ecliptic, and the blue line the horizon.
3) When standing anywhere along the equator, the zenith will be located on the line of the celestial equator; in this case, the horizon line will necessarily intersect the northern and southern poles of the Earth. See diagram 3, where the perspective is that of an observer located on the equator of the Earth. Here, the black line is the equator, the red line the ecliptic, and the blue line the horizon.
All three diagrams are representations of the position of the sun as described in Inferno 1.37-41, that is, on the day of the vernal equinox, but each presents the position of the sun from three different earthly locations. This planetary snapshot represents the time indicated at the beginning of Inferno 1, but underscores the text’s lack of specificity regarding the purported locus of observation: the dark wood is ostensibly somewhere between the northern pole and the equator, meaning that diagram 2 is the most accurate representation of the opening shot of the heavens in the Commedia, but the precise location of this observation of the sun is never given. This lack of certainty regarding the observational astronomy in Inferno stands in contrast to the geographic specificity inherent in Purgatorio. Moreover, in thinking ahead, note that diagram 2 is the only model of the cosmos that captures the essence of the astronomical reference in Paradiso 1, where three distinct circles must run perpendicular (or nearly perpendicular) to the meridian in order to form the “tre croci” which Dante mentions (v. 39).
Inferno 2.76-78
O donna di virtù, sola per cui
l’umana spezie eccede ogne contento
di quel ciel c’ha minor li cerchi sui,
(Inf. 2.76-78)
For the majority of Inferno 2 (specifically, vv. 43-126), Virgil recounts a story about his encounter with Beatrice, providing a pre-history for the start of the poem in Inferno 1. It is in the midst of this story that Virgil introduces the poem’s next astronomical periphrasis, “quel ciel c’ha minor li cerchi sui” (Inf. 2.78), and, in doing so, begins building out in earnest the cosmological framework that will ultimately bolster the setting of Paradiso.
In this project I am focused on tracking the information that Dante provides for his reader in the places where he provides it, referencing source material when necessary in order to provide a historicized context for understanding the cosmic system that the poet crafts as a structure for his imagined world. Like any literary world, Dante’s imagined cosmos does not simply appear; rather, the poet builds it in time using a number of tools, astronomy chief among them. To better capture this stepwise process of poetic creation, I do not want to anticipate in this project any of the poet’s inventions merely because they have become so rooted in our imaginary as repeat readers of the Commedia. The spectacular craft of the poet’s world-building is often veiled by astronomical periphrases and discourses on the heavens, and to anticipate this gradual process is to bulldoze the experience of poetic artifice. It is for this reason that my diagrams do not yet feature Mount Purgatory. For a more elaborated explanation of the reasons behind this choice, see my Note on Method of Presentation.
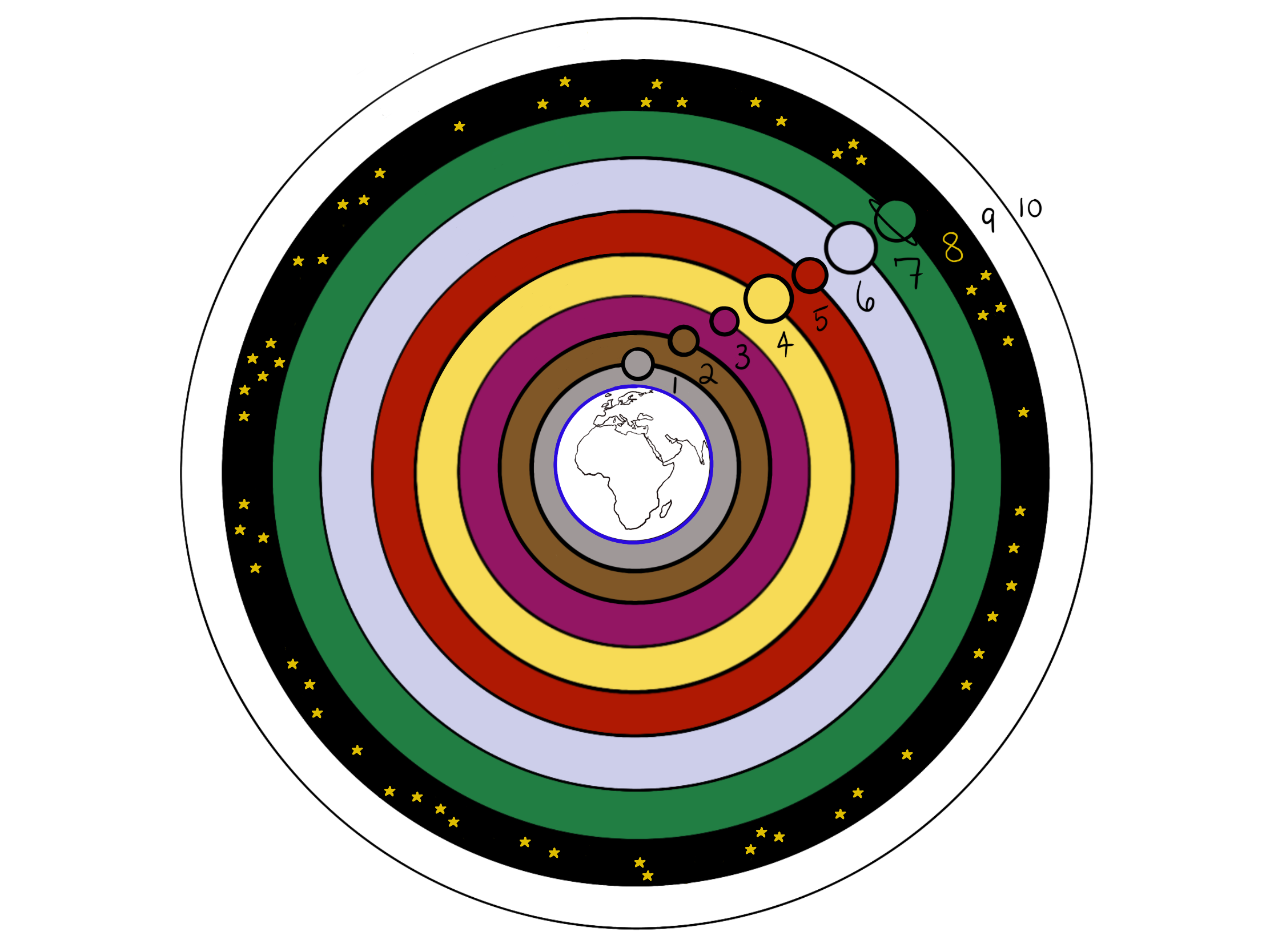
The astronomical reference in Inferno 2, “quel ciel c’ha minor li cerchi sui,” is a periphrasis for the heaven of the moon. This verse is by no means emphasized in the canto: it immediately follows Beatrice’s climactic speech (vv. 58-76), it is presented only in an appositive to “donna di virtù,” and, after uttering it, Virgil quickly moves to accept his charge and ask Beatrice a question (vv. 79-84) that is unrelated to the moon. Nonetheless, this verse provides useful insight to the poet’s model cosmos, and, accordingly, the narrative that unfolds within it. On the whole, Dante’s cosmos consists of manifold spherical domains which, as he emphasizes in this verse, are composed of a set of theoretical circles that are proportionate in size to the sphere that contains them. Nestled like Russian dolls encapsulating the earth, the heavenly spheres are diaphanous, physical entities which increase in size from the moon up to the Primo Mobile, the outermost perceptible sphere lying beyond the heaven of the fixed stars. The Empyrean—an eternal heaven which is imperceptible—is beyond the Primo Mobile. Dante first articulated this model of the cosmos in the Convivio. In Convivio 2.3.7-8 Dante outlines his thoughts on the ordering of the heavens:
Ed è l’ordine del sito questo, che lo primo che numerano è quello dove è la Luna; lo secondo è quello dov’è Mercurio; lo terzo è quello dov’è Venere; lo quarto è quello dove è lo Sole; lo quinto è quello di Marte; lo sesto è quello di Giove; lo settimo è quello di Saturno; l’ottavo è quello de le Stelle; lo nono è quello che non è sensibile se non per questo movimento che è detto di sopra lo quale chiamano molti Cristallino, cioè diafano, o vero tutto trasparente. 8. Veramente, fuori di tutti questi, li cattolici pongono lo cielo Empireo, che è a dire cielo di fiamma o vero luminoso; e pongono esso essere immobile per avere in sé, secondo ciascuna parte, ciò che la sua materia vuole.
[The order of their position is as follows. The first in number is the one in which the Moon resides; the second is the one in which Mercury resides; the third is the one in which Venus resides; the fourth is the one in which the Sun resides; the fifth is that of Mars; the sixth is that of Jupiter; the seventh is that of Saturn; the eighth is that of the Stars; the ninth is the one which is not perceptible to the senses except for the movement mentioned above, and which many call the Crystalline (that is to say, the diaphanous or completely transparent) Heaven. Moreover, outside all of these the Catholics place the Empyrean Heaven, which is to say, the “heaven of flame,” or “luminous heaven”; and they hold it to be motionless because it has in itself, with respect to each of its parts, that which its matter desires (Lansing).]
Accordingly, the moon is the smallest of the heavenly spheres, and hence it is composed of the smallest circles. This is the first of the heavens that the pilgrim will traverse in Paradiso. The use of “ciel” in Inferno 2.78—rather than “stella” or “pianeta”—and the emphasis in Convivio 2.3.7-8 on the difference between the planets and their heavens together underscore the fundamental notion that each of the seven visible planets “resides” on the surface of the diaphanous spheres which constitute the heavens. This distinction is important: the heaven of the moon is the sphere that is concentric with the earth and whose radius is measured by the distance from the center of the earth to the moon; the moon, alternatively, is the sole star that is located on the surface of the heaven of the moon, which is the smallest celestial sphere.
All of the planets and stars in this cosmic system are therefore like radiant blemishes on the translucent surfaces of these nestled, concentric spheres. “[O]gne contento / di quel ciel c’ha minor li cerchi sui,” then, refers to everything that exists within the volume of this sphere: namely, the four elements (earth, water, air, and fire). In other words, this verse refers to the sublunar world of ephemera in which perceptible objects are subject to time and, excepting those who dwell in Hell, to change. Dante uses a similar locution in Inferno 7.64, when he says “[…] tutto l’oro ch’è sotto la luna.”
Inferno 7.97-99
Or discendiamo omai a maggior pieta;
già ogne stella cade che saliva
quand’ io mi mossi, e ’l troppo star si vieta.
(Inf. 7.97-99)
Virgil declares in Inferno 7.98-99 that “già ogne stella cade che saliva / quand’ io mi mossi.” The impact of the utterance is straightforward: the time has come for the pilgrim and his guide to move on to the subsequent circle of Hell. The wording of this expression, however, presents two issues, one that is epistemic and one that is interpretive. The first issue, which I wish to emphasize but set aside for the moment, is that it is unclear how Virgil can know that the stars, which were rising when he first moved, are now falling. As the reader learns in Inferno 3.22-23, it is impossible to see the stars in Hell: “Quivi sospiri, pianti e alti guai / risonavan per l’aere sanza stelle” (my emphasis). Virgil’s evident ability to track the movement of the stars throughout Inferno implies that there is some mechanism by which he can intuit the movement of the heavens even though he cannot perceive this movement directly. Dante never indicates how this is possible, nor whether this is a power that is specific to Virgil or something that is shared among the damned.
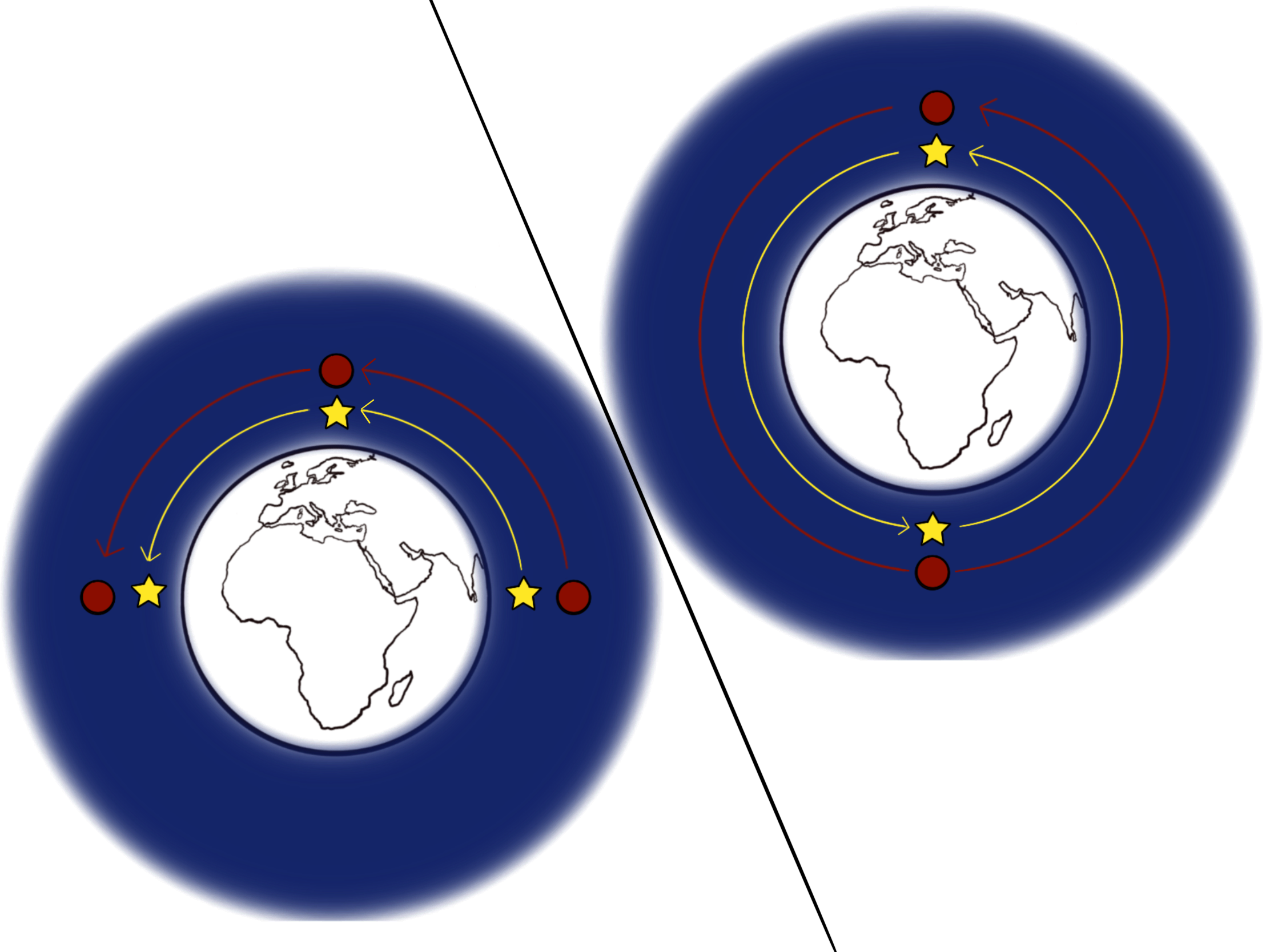
The second issue, which is interpretive by nature, regards the terms “cade” and “saliva.” How we ultimately understand and gloss these terms bears on how we can contextualize Virgil’s “mi mossi” within the larger narrative. Astronomically speaking, there are two ways in which the terms “cade” and “saliva” can be read: one from a horizontal perspective and one from a global perspective. In the diagram above, “horizontal interpretation” and “global interpretation” are terms I use for the sake of clarity, as I have not seen any standard nomenclature used regarding these interpretations. Buti and Bertagni, for example, side with the global interpretation, arguing that “[c]ade e saliva non possono riferirsi ad un orizzonte (in questo caso all’orizzonte di Gerusalemme […]) e indicare il ‘sorgere’ e il ‘tramontare’ delle stelle” (page 79).” Edward Moore, differently from Buti and Bertagni, pushes for the horizontal interpretation, and does not mention the possibility of a “global interpretation” at all (page 42).
On the horizontal interpretation (left diagram), we would consider only the stretch of visible sky that extends from the eastern to the western horizon at a given observational locus (Buti and Bertagni assume that the horizontal interpretation would have to posit Jerusalem as the observational center, and this is for reasons that will become clearer in Purgatorio). Critics who take the horizontal view interpret “saliva” as indicating a period of 6 hours during which the stars rise from the eastern horizon to their highest point in the sky, and “cade” as indicating an equivalent period of 6 hours during which the stars fall from the zenith to the line of the western horizon. While a neat option, there is a fundamental issue with the horizontal interpretation. First, from most observational loci on earth, there is an apparent asymmetry regarding the stars’ path over the horizon. Some stars, like the sun during the equinox, do appear to rise for roughly 6 hours and fall for another 6 regardless of one’s location. But some of the fixed stars are located closer to the northern celestial pole, and never actually fall below the horizon, while some other stars are located closer to the southern celestial pole, and only ever rise above the horizon for a brief period of time each day. In sum, not every star in the sky crosses the horizon, rises for 6 hours, falls for another 6 hours, and then crosses the horizon again like the sun: depending on the position of the stargazer, certain stars will rise and fall for 10 hours, while certain others will only rise and fall for 4. In fact, certain stars at a given location will never dip below the horizon, and will instead appear to rise for 12 hours and fall for another 12, hanging perpetually in the sky, while others will never cross the horizon to rise or fall at all. For this reason, the horizontal interpretation relies on a problematic reduction of reality, one which posits an idealized revolving sky that features the uniform rising and setting of every star. The horizontal interpretation cohere in just one particular observational instance: namely, when the rotational axis (the axis connecting the northern and southern poles of the Earth) is coplanar to the horizon—which is to say, when the observational locus is the equator itself (where the poles are on the horizon, and therefore everything in the sky would appear to rise and fall equivalently). As Buti and Bertagni argue, however, for observers at any other location it is incoherent to say “saliva” and “cade” and intend “were rising” and “are now falling,” and this is because the stars would appear rise and fall at asymmetric intervals, ranging from just a few minutes to 12 hours in one direction.
The issue with the horizontal interpretation, then, is entirely technical: it presents a reduction of the world’s cosmic system that is only coherent at the equator (a place which, by Inferno 7, we know the pilgrim and his guide are not). The technical problem aside, the horizontal interpretation implies that Virgil’s “mi mossi” is in reference to an event 6 hours in the past. Those who side with the horizontal interpretation claim that “mi mossi” refers neatly back to Inferno 1.136 and Inferno 2.1, where Dante states clearly “[a]llor si mosse, e io li tenni dietro” (my emphasis) and then “[l]o giorno se n’andava, e l’aere bruno […],” making Virgil’s utterance a declaration that 6 hours have passed (that is, from evening to midnight) over the course of the journey from Inferno 2.1 until the present passage. This interpretation is bolstered by the elegant connection supplied by the repeated verb: “si mosse” in Inferno 1.136 becomes “mi mossi” in Inferno 7.99. As such, the horizontal interpretation amounts to the indication that it’s now just after midnight, 6 hours having passed since Dante and Virgil first left the selva oscura at the close of Inferno 1/start of Inferno 2.
On the global interpretation (right diagram), we account for the entirety of the motion of the stars around the earth in the Ptolemaic model cosmos. This view removes the central observational locus altogether and thereby eliminates the relevance of the horizon: we consider only that the stars encircle the earth fixedly, and note that they must rise from their southernmost point to their northernmost point in 12 hours, and descend back over the course of another 12 hours. The global interpretation is, strictly speaking, the more technically correct in astronomical terms. Under a total view of the moving Ptolemaic cosmos, to say that every star which was then rising is now falling is to say that 12 hours have passed, since some stars would have just begun their northern ascent at the moment indicated by “mi mossi.” That being said, those who side with the global interpretation have a much more complicated interpretive hurdle: there is no unproblematic way to place “mi mossi” in the progression of “fabula” or narrative time that is provided by the text. Critics who prefer the global interpretation find themselves somewhat hamstrung due to the next indication of fabula time in Inferno 11.112-114, where we will see that it is still before sunrise. Since the sun will rise around 6:00am given the proximity of the equinox, “mi mossi” cannot refer to Inferno 1.136 on the global interpretation: for a duration of 12 hours following that moment would effectively postdate Inferno 7.97-99 to Inferno 11.112-114. With this in mind, ultimately, the upshot of the global interpretation has to be more or less the same as that of the horizontal interpretation: it is still going to have to be just after midnight in Inferno 7.97-99, irrespective of how we gloss the particularities of “cade” and “saliva.” So, in the end, the only substantive difference between the horizontal and global interpretations is the assertion that, on the global interpretation, “ogne stella cade che saliva” means, on a purely technical level, that 12 hours have passed since some indeterminate moment when Virgil first moved from Limbo at Beatrice’s behest, rather than 6 hours since Inferno 1.136.
Buti and Bertagni’s Commento astronomico della ‘Divina Commedia’ is an incredibly instructive survey of astronomy in the Commedia. In this particular instance, however, it seems that the desire to read a rigid, scientific technicality in the poet’s craft has led to rather strange conclusions. Buti and Bertagni claim that “mi mossi” does still refer to Inferno 1.136, but that it is midday at the close of the first canto and there are an inexplicable “6 ore ‘vuote’” (page 81) between Inferno 1.136 and Inferno 2.1 (one imagines Virgil and Dante must, on this reading, have spent six hours chatting about poetry before the events of Inferno 2 commence). Others who side with the global interpretation claim instead that “mi mossi” is a reference back to an event that precedes the action of Inferno 1: namely, what is mentioned in Inferno 2.118, “E venni a te così com’ ella volse,” the moment when Virgil first moved from Limbo. This latter solution is certainly preferable to leaving 6 hours unaccounted for between Inferno 1.136 and Inferno 2.1, but the reference feels far too vague and uncertain when compared to the precise lexical repetition of “si mosse” in Inferno 1.136 and “mi mossi” in Inferno 7.99. At any rate, it quickly begins to feel like one is needlessly splitting hairs by forcing the global interpretation when the outcome, as regards Inferno 7, is precisely the same in either case: it is now just after midnight.
Given that the information value of the two interpretations yields identical results, siding with one or the other is ultimately immaterial. But the spirited and centuries-long desire to reconcile these verses to a particular temporal map of the journey does underscore the extent to which astronomy is continuing to serve Dante as a buttress to the poem’s mimetic effect. The rising and setting stars are brought into the poem as a narratological sleight of hand: in highlighting the movement of the stars across Inferno (which no character in the narrative can actually see), Dante manages to make the poem appear as if grounded in time. The mention of rising and falling stars and the narrative past spurs the attentive reader to try to weave these time references together in such a way as to locate the progression of the journey within history. For this reason the stars of Inferno, which are at bottom no more than indications of fabula time in the imagined cosmos, look like poetic moorings to the progress of history.
If we want to try our hand at locating the poem in historical time, up to this point our clues to the date and time of the poem are the following.
(1) This journey takes place in the middle of Dante’s life (Inferno 1.1), therefore between 1265 and 1321. The year 1300 stands out as the obvious choice, particularly in the context of Convivio 4.23.9-10:
Là dove sia lo punto sommo di questo arco [della vita], per quella disaguaglianza che detta è di sopra, è forte da sapere; ma nelli più, io credo, tra il trentesimo e ‘l quarantesimo anno; e io credo che nelli perfettamente naturati esso ne sia nel trentacinquesimo anno. E muovemi questa ragione: che ottimamente naturato fue lo nostro Salvatore Cristo, lo quale vollemorire nel trentaquattresimo anno della sua etade; ché non era convenevole la divinitade stare in cosa [in] discrescere […].
[It is difficult to determine where the highest point of this arc lies, because of the inequality mentioned above, but in most lives I believe it is attained between the thirtieth and fortieth year, and I believe that in those whose nature is perfect it is attained in the thirty-fifth year. My belief is compelled by the argument that our Savior Christ had a perfect nature and desired to die in the thirty-fourth year of his life, because it would not have been fitting for a divinity to enter into such a decline as this. (Lansing)]
(2) It is springtime, on or around the day of the vernal equinox (Inferno 1.37-40).
(3) It has just passed midnight on the first day of the journey (Inferno 7.97-99). The journey began in the morning in the selva oscura (Inferno 1.37), and it was already nightfall by the opening of the second canto (Inferno 2.1).
Interpretation of Inferno 7.97-99 by Authoritative Commentators:
| Horizontal Interpretation (see note to Inferno 7.98) | Global Interpretation (see note to Inferno 7.98) |
| Jacopo Alighieri, Jacopo della Lana, L’Ottimo Commento, Boccaccio, Benvenuto da Imola, Francesco da Buti, Anonimo Fiorentino, Cristoforo Landino, Alessandro Vellutello, Lodovico Castelvetro, G.A. Scartazzini, Tommaso Casini and S.A. Barbi, G.A. Scartazzini and G. Vandelli, Luigi Petrobono, Attilio Momigliano, Charles Singleton, Anna Maria Chiavacci Leonardi, and Robert Hollander. See also Edward Moore’s 1887 Time-References in the Divina Commedia (page 43). | Natalino Sapegno, Daniele Mattalia, Siro A. Chimenz, Giorgio Padoan, and Umberto Bosco and Giovanni Reggio. See also Buti and Bertagni’s 1966 Commento astronomico della Divina Commedia (pages 79-81) |
N.B: All commentaries accessed via dante.dartmouth.edu.
Inferno 10.79-81
Ma non cinquanta volte fia raccesa
la faccia de la donna che qui regge,
che tu saprai quanto quell’ arte pesa.
(Inf. 10.79-81)
In Inferno 10 Farinata degli Uberti provides the pilgrim the following prophecy: within fifty full moons, you will know the difficulty of returning from exile. Despite its importance, the prophecy’s historical claim to Dante’s experience of exile lies outside the scope of this astronomical study. My focus here is on the indication of time Farinata uses: fifty lunar cycles. The moon is implicated by the periphrasis, “fia raccesa / la facia de la donna che qui regge,” the reference being to Proserpina, a goddess traditionally associated with the moon. The inquiry regards the length of fifty full moons.
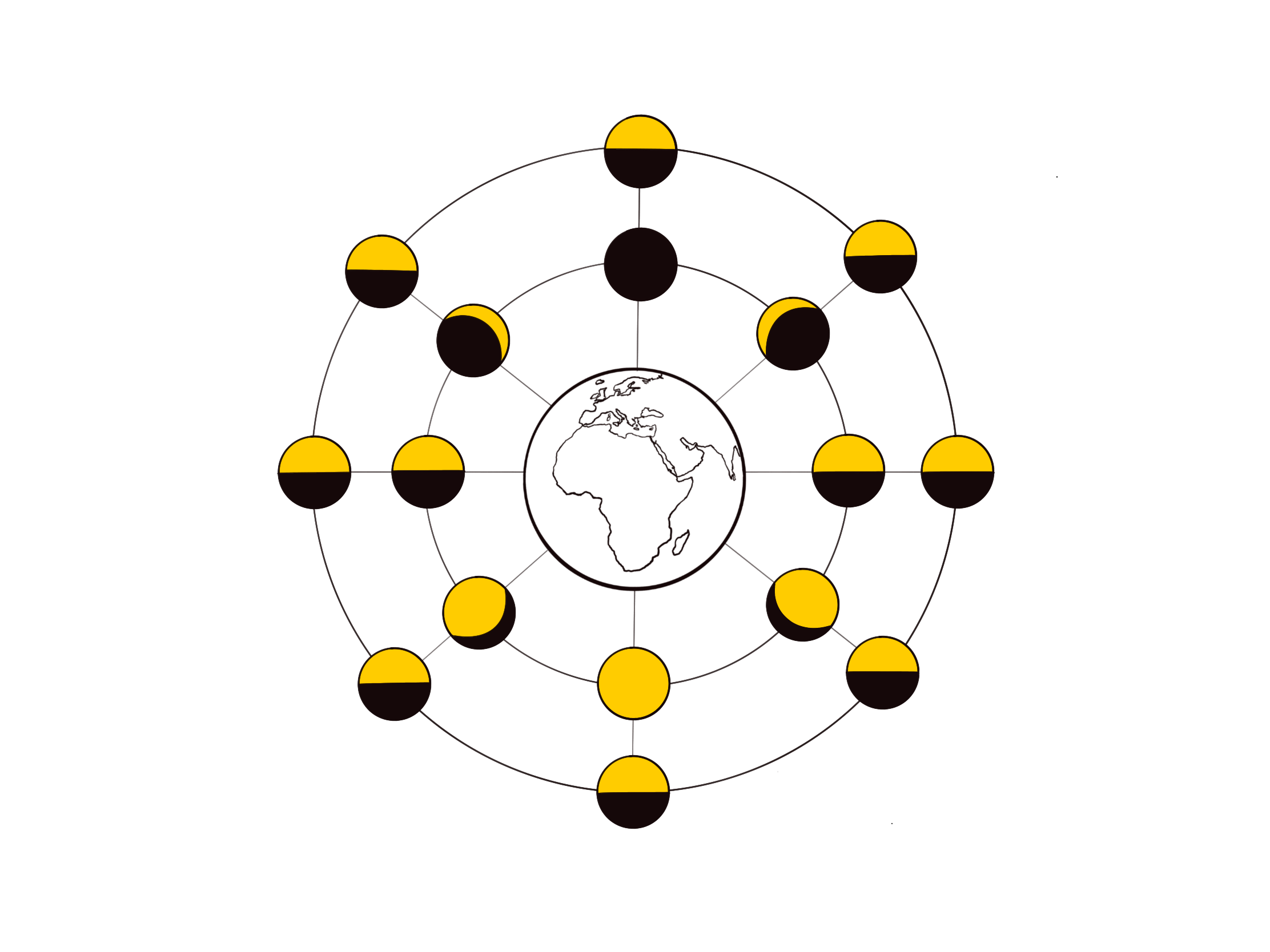
Unlike the sun, the moon does not shine with its own light. The phase of the moon is determined by its position relative both to the sun and to the earth. A new moon appears in the sky when the moon stands between the sun and the earth without causing a solar eclipse; likewise, a full moon appears in the sky when the moon stands opposite the sun, with the earth between them in such a way as not to cause a lunar eclipse. The intermediate phases (crescent, quarter, half, gibbous) are intervals in the relative movement of the sun and moon taken from the perspective of earth. In the diagram above, adapted from Buti and Bertagni’s diagram for the phases of the moon (page 44), the outer circle represents a total view of the moon (i.e., how the light of the sun is striking it) while the inner circle shows the appearance of the moon from the perspective of earth, and therefore the lunar phases.
We can ascertain the length of a single lunation either with a somewhat lengthy observation, or by means of a quick observation and some simple calculations. The former method is rather intuitive: we could just count the days from one full Moon to the next, which would turn out to be a period of approximately twenty-nine days, and then multiply by 50. So, 29 [days from one full moon to the next] x 50 [full moons] = 1450 days / 365 [days per year] = roughly 4 years. This, then, is the length of time indicated by Farinata’s prophecy.
The other method mentioned above is more precise and, though requiring more math, takes less time to yield the same result. On any given night, we could step outside at midnight and mark the location of the moon in the sky, relative to the nearest star (and perhaps using an astrolabe to measure the distance). Recalling that the moon is one of the “wandering stars” while the constellations are “fixed stars,” we could step outside on the following night at the same time and mark the new location of the Moon relative to that same star. While everything in the sky—including the fixed stars—spins about the celestial polar axis each day from east to west, only the wandering stars also appear to move about the ecliptic from west to east. So over the course of this 24 hour period (and with the help of an astrolabe) we would find that the moon appears to have traveled a distance of approximately 13-degrees about the 360-degree ecliptic (see Buti e Bertagni, page 43; see also Brunetto Latini: “Ora è leggier cosa a sapere in che segno rimane lo Sole. E poi che l’uomo sa ciò, e’ può leggermente sapere ov’è la Luna, chè ella si dilunga ciascun dì dal Sole 13 gradi […],” book II, cap XLIX). We could make this same observation for the sun by noting the stars rising just before sunrise or setting just after sunset, and note that the sun, too, is traveling eastward along the ecliptic at a pace of about 1-degree per day.
Now, with this information in mind we can calculate the length of the full lunar cycle. As the diagram above highlights, the moon is full when it is located 180-degrees opposite the sun, which we can take as our starting point. From here, for the moon to be full again, it will need to travel at least another 360-degrees: 360 [degrees] / 13 [degrees per day] = approximately 27.5 days. If the sun were to be stationary in the sky, then the lunar cycle would be 27.5 days. Since the sun is not stationary, and instead appears to be moving at a rate of 1-degree per day, the moon will have to surpass the previous location of the full moon by the distance traveled by the Sun in that same amount of time. In the time it takes the moon to circle the entire ecliptic, the Sun, traveling 1-degree per day, will have traveled another 27.5-degrees. Accordingly, at a rate of 13-degrees per day, the moon will come to reach its position precisely opposite the sun again in a little over two days’ time. We arrive at the same conclusion: the lunar cycle is a period of approximately 29.5 days, again indicating that fifty full Moons will occur in a period of roughly four years.
In the previous section I made the point that Virgil, like all souls within Hell, cannot see the stars per the “aere sanza stelle” of Inferno 3. For this reason I think it is worth highlighting that in Inferno 10 Farinata does not need to be able to see the stars in order to make this statement. Different from Virgil’s time references, which appear to be direct and present observations of the heavens, Farinata’s utterance relies on knowledge about the heavens (i.e., the length of a lunation) but not any immediate or direct observation. Farinata does explain to Dante toward the end of this canto that he and the other damned souls are able to see the future when it is distant, but not the present or the past —
“Noi veggiam, come quei c’ha mala luce,
le cose”, disse, “che ne son lontano;
cotanto ancor ne splende il sommo duce.
Quando s’appressano o son, tutto è vano
nostro intelletto; e s’altri non ci apporta,
nulla sapem di vostro stato umano.
(Inf. 10.100-105)
— but this does not seem to shed any light on the epistemic problem regarding observation of the heavens throughout Inferno. Farinata imparts his prophecy regarding Dante’s exile several years in advance by using the moon as a timepiece, but this does not at all imply that he can see how the moon tracks across the sky during this time. A span of 50 lunar cycles is a set amount of time, equivalent to any other method of denoting a particular length of time (4 solar returns, etc.). In fact, that a character in the text is able to make reference to the passage of time while under a sky with no stars seems to suggest that Dante has more of an Augustinian view of time, namely, that the relation between time and the stars is accidental. At any rate, the epistemic issue remains unresolved.
Inferno 11.112-114
Ma seguimi oramai, che ’l gir mi piace;
ché i Pesci guizzan su per l’orizzonta,
e ’l Carro tutto sovra ’l Coro giace,
(Inf. 11.112-114)
Readers of Dante in the 21st century face a host of challenges, some linguistic and others cultural. Perhaps it is strange to consider that one among these challenges is a direct result of light pollution. Short of traveling to a designated dark sky zone, it is near impossible to fathom the night sky as it once appeared, unencumbered by the glow of artificial nighttime lighting. Of course, this was the norm for Dante and his contemporaries, who enjoyed the nightly show of roaming, constellated skies in perfect, primordial darkness. Today, however, it is reported that 83% of the global population lives beneath light polluted skies (Energy.gov)—our “notte privata / d’ogne pianeto” caused, perhaps paradoxically, not by the “buio d’inferno,” but by our love for shining light.
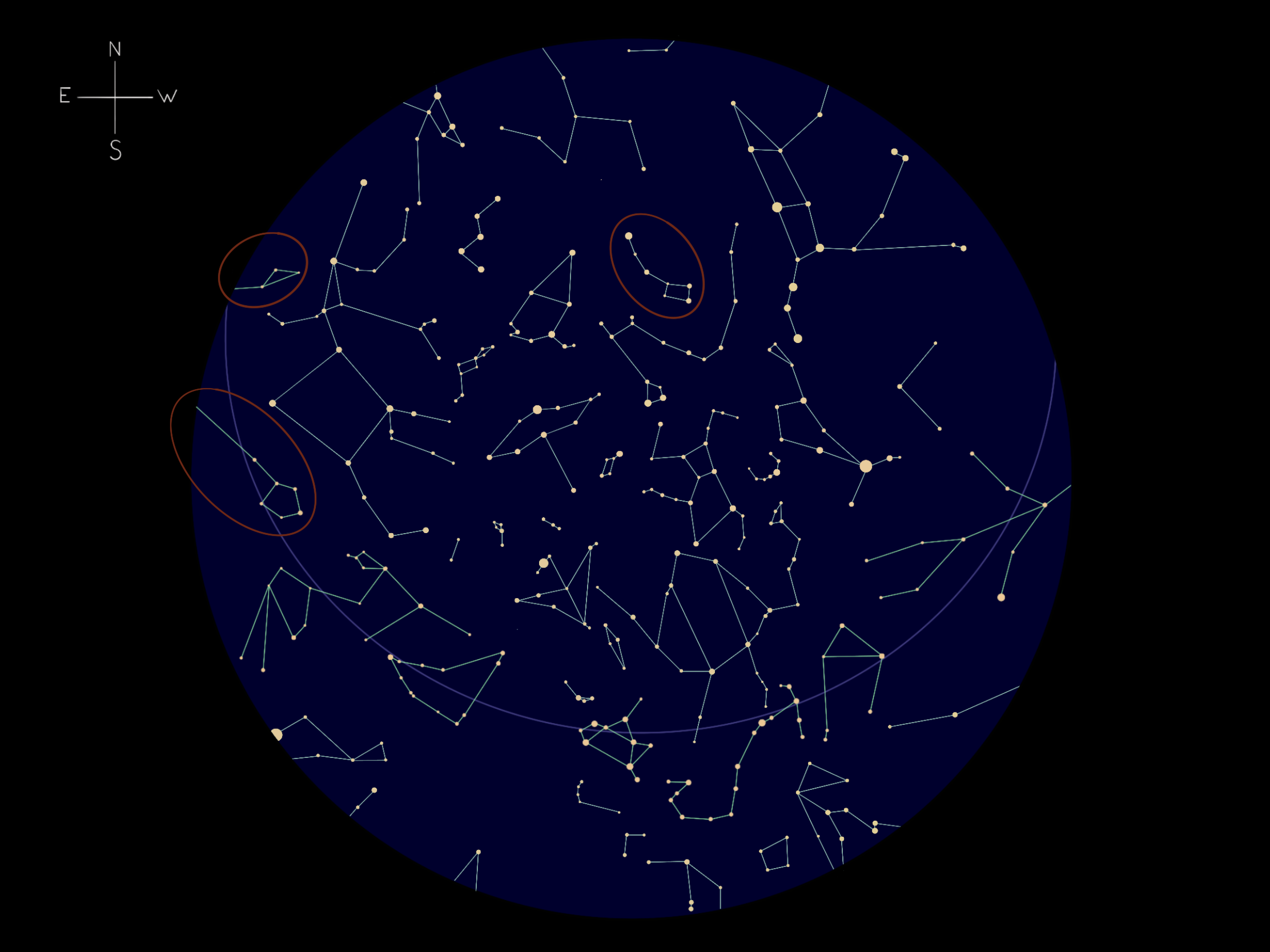
Virgil provides a snapshot of the night sky in Inferno 11.112-115, the fourth indication of fabula time in the poem (following Inferno 1.37-41; Inferno 2.1; Inferno 7.97-99). The information of these verses is that Pisces is just now glittering above the horizon, while the Wagon (Ursa Major) lies over Caurus (the north-western wind). To determine the time indicated by this utterance, we must recall that the sun is in Aries, the first sign of the zodiac. Pisces, on the other hand, is the twelfth and final sign of the Zodiac, making it the sign that rises above the horizon just before Aries does. With Pisces on the horizon in Inferno 11, we can determine that the sun (in Aries) still has not yet risen.
While a solar day is the amount of time it takes for the earth to rotate such that the sun appears to travel from the meridian (the highest point in the sky; noon) on one day to the meridian on the next, a sidereal day is the amount of time it takes for the earth to rotate such that any of the fixed stars appears to travel from meridian to meridian. The difference between a solar day and a sidereal day is equal to the quotidian differential caused by the sun’s annual motion. Recall that everything in the sky appears to rise on the eastern horizon and move westward due to the earth’s rotation; in the Ptolemaic model of the cosmos, however, there is no recognition of this fundamental cause for celestial movement. As such, the sun is a “wandering” star that—in addition to the basic westward movement of everything in the sky—also appears to move from west to east at a rate of approximately 1-degree per day. For this reason the solar day is just slightly longer than the sidereal day, which is only 23 hours and 56 minutes long.
Given that it takes 23 hours and 56 minutes for the fixed stars to appear to make one full rotation and complete a sidereal day, a new sign of the zodiac must appear on the eastern horizon just under every two hours. Therefore, with Pisces just now darting over the horizon, we are about two hours from sunrise. The location of Pisces alone would be enough to indicate the general time at this point in the journey, though we are also given information about Ursa Major (“’l Carro”). The diagram above is an approximate depiction of all the stars which appear in the sky above Jerusalem in the spring, moments before sunrise. The two which Virgil chooses to highlight are marked: (1) Pisces darting over the horizon, evidenced in two circles on the left of the diagram and (2) the carro—“wain” or “wagon,” i.e. Ursa Major—located in the northwestern quadrant. The light purple line that passes through the diagram as a partial circle denotes the ecliptic, which of course is not a visible line in the sky, but a theoretical one imagined in order to aid mathematical astronomy.
Boccaccio in his Esposizioni sopra la commedia di Dante (accessed via dartmouth.dante.edu) echoes the precise language used by Isidore to describe the northwestern wind, Caurus:
Boccaccio: “l’ottavo [vento] chiamano ‘coro’ o vero ‘maestro’, il quale è tra ponente e tramontana: e chiamasi coro per ciò che compie il cerchio, il quale viene ad essere in modo di coro, cioè di quella spezie di ballo il quale è chiamato ‘corea’.” (ad locum)
Isidore: Corus est qui ab occidente aestivo fiat. Et vocatus Corus quod ipse ventorum circulum claudat, et quasi chorum faciat. [Corus is the one that blows from the west in the summer, and it is called Corus because it closes the circle of winds, and makes them like a ring-dance (chorus) (Barney, et al. translation)] (book XIII, xi)
If we were able to see the sky adorned with the lights of the firmament, we could sit and watch at night as these stars spin from east to west around the lodestar, Polaris, which marks the northern pole of the celestial axis. Indeed, there can be no doubt that, from time to time, Dante himself would have sat to admire the nightly spectacle.
Inferno 20.124-129
[diagram]
Ma vienne omai, ché già tiene ’l confine
d’amendue li emisperi e tocca l’onda
sotto Sobilia Caino e le spine;
e già iernotte fu la luna tonda:
ben ten de’ ricordar, ché non ti nocque
alcuna volta per la selva fonda”.
(Inf. 20.124-129)
This passage marks the fifth reference to fabula time in the Commedia, and the third time that Virgil calls the pilgrim to the attention of passing time. Virgil’s time references distinguish themselves from the narrator’s in that they are dialogic. The observation of morning and the rising sun in Inferno 1.37-40 is presented in the voice of the narrator and as such carries the implication, given the poetic fiction, of being an image from the poet’s store of memory, one that aims at an approximation of what the pilgrim purportedly saw on his lost day in the dark wood. The “Virgilian” time references, differently from the narrator’s, are the pronouncements of a character in the fiction and marked by the expressly dialogic adverb “omai” (equivalent in Inferno 7.97; Inferno 11.112 has a variant, “oramai”). Insofar as dialogue, Virgil’s time-references carry the implication of being a present observation of the moving heavens: he appears to notice that a given star has arrived at a given location, and he offers this as motivation for the pilgrim to move along.
As I highlighted above in my commentaries to Inferno 7.97-99 and Inferno 10.79-81, any claim that Virgil makes to an open sky presents a glaring epistemic problem. The epistemic problem that haunts any passage entailing “observational” astronomy from Inferno 3.23 to Inferno 34.136 is directly and repeatedly engendered by the fiction. In the first place, the poet foregrounded deliberately in Inferno 3 that Hell’s skies are devoid of stars. The choice, then, to stage a character’s observation of the skies again and again creates tension, if not an inconsistency, across the first cantica. But this basic problem expands and redoubles as the journey progresses. In the passage we are presently considering, for example, Virgil spots the moon (“Caino e le spine”) on the western horizon, touching the border of the hemispheres upon the waves beneath Seville (“tiene ’l confine / d’amendue li emisperi e tocca l’onda / sotto Sobilia”), while such an observation has to be geometrically impossible. Dante’s imagined world places Hell in an abyss within the earth, hence the two protagonists will—especially by Inferno 20—have traveled quite far below the earth’s surface. The deeper one progresses toward the center of the earth, the more shallow one’s view of the sky becomes, and at any depth greater than one’s line of vision the horizon vanishes from sight. Even if we set aside the totalizing indication of a dark sky in Inferno 3, the narrative setting precludes the optical possibility of Virgil’s observing anything on the horizon at any point between Inferno 3 and the second half of Inferno 34. Yet Virgil has claimed to observe something on the horizon twice now: pisces on the eastern horizon in Inferno 11, as we just saw, and now again the moon on the western horizon in Inferno 20. Each time Virgil makes any astronomical observation in Inferno—and particularly when he gestures to this phantom horizon—it should add to our sense of this inherent temporal tension in the first cantica.
The epistemic issue aside, this passage gives us two key pieces of information (neither of which offers any resolution). The two pieces of information are: 1) the journey began under a full moon the night before, and 2) it is presently around 6:00am, as the moon is setting in the west and therefore the sun must be just about rising in the east.
Inferno 29.10-12
[diagram]
E già la luna è sotto i nostri piedi;
lo tempo è poco omai che n’è concesso,
e altro è da veder che tu non vedi”.
(Inf. 29.10-12)
The first verse of this passage is taken to indicate a time in the early afternoon. There is, yet again, an inherent complication in parsing this verse, one which the text creates and does not resolve. “E già la luna è sotto i nostri piedi” is a clear indication that the sun, opposite the moon, is somewhere around the midheaven, or high noon. Given that the moon is placed “beneath our feet” at the imum coeli, it cannot be exactly noon, but must be a little bit past since the moon travels more quickly than the sun (recalling that the moon slides eastward 13 degrees/day while the sun only shies eastward at a rate of 1 degree/day). The full moon was “iernotte” as of Inferno 20, so considering the progressive eastward differential of 12 degrees each day, the moon will be offset an exact opposition with the sun by 12 degrees per day following the lunation. But the essential question—how many hours have passed between the “iernotte” of Inferno 20 and this passage from Inferno 29?—cannot definitively be answered.
If we try to follow the iterative time references across Inferno in order to determine how much time has passed from the full moon, we arrive at an inherently equivocal conclusion. The data are as follows. The sun was rising in Inferno 1, and it was the morning (“[t]emp’era dal principio del mattino”). By the first verse of Inferno 2, it is dusk (“lo giorno se n’andava”). In Inferno 7 we find that the stars which were previously rising are now falling, which must ultimately mean—irrespective of the interpretive challenges posed by the verse—that it is around midnight (or, if any later, still before sunrise). Inferno 11 highlights that it is around 2 hours before sunrise, while Inferno 20 indicates that it is just before sunrise. This passage from Inferno 29 pushes the clock ahead yet again: it is now around 1:30pm. Synthesizing the time references, the clock of Inferno might move as follows.
Inferno 1.37-40: sunrise, day 1
Inferno 2.1: evening, day 1 (+12 hours from previous time reference)
Inferno 7.97-99: just after midnight, day 2 (+6 hours; +18 hours total)
Inferno 11.112-114: ~2 hours before sunrise, day 2 (+4 hours; +22 hours total)
Inferno 20.124-129: just before sunrise, day 3 (+26 hours; +48 hours total)
Inferno 29.10-12: afternoon, day 3 (+7.5 hours; +55.5 hours total)
Some, however, argue that we should condense the above time frame as follows.
Inferno 1.37-40: sunrise
Inferno 2.1: evening, day 0
Inferno 7.97-99: just after midnight, day 1 (+6 hours)
Inferno 11.112-114: ~2 hours before sunrise, day 1 (+4 hours; +10 hours total)
Inferno 20.124-129: just before sunrise, day 1 (+2 hours; +12 hours total)
Inferno 29.10-12: afternoon, day 1 (+7 hours; +19 hours total)
The determining issue here is how one construes the passage of time between Inferno 11.112-114 and Inferno 20.124-129: the former indicates that it is approximately 2 hours before sunrise while the latter tells the reader it is just moments before sunrise. But do 2 hours pass, or 26? On the one hand it might seem odd that Dante would let such a small amount of time (2 hours) pass over the course of 10 canti (from Inferno 11 to 20) after having just indicated clearly that 10 hours have passed over the course of an equivalent amount of textual space (Inferno 2.1 to Inferno 11.112). And the fact that approximately 12 hours then pass between Inferno 20.124-129 and Inferno 34 only emphasizes the strangeness of what would appear to be an inconsistently brief interval of fabula time in the central third of Inferno. On the other hand, it might seem odd to suppose that 26 hours pass from Inferno 11 to Inferno 20, when only 10 hours pass from Inferno 2 to Inferno 11 and only 12 from Inferno 20 to Inferno 34. In this case, an inconsistently lengthy interval of fabula time would comprise the middle third of the text. Neither case is particularly compelling, but the discomfort cannot be avoided: either fabula time drastically dilates and slows through the central third of Inferno, or it radically and temporarily hastens only to return to a pace in the final third that approximates that of the first.
Accordingly, the timeline is equivocal, and there is no key in the text that can resolve the equivocation. In this way, depending on how we situate the time reference at the end of Inferno 20 within the encircling context provided by Inferno 11.112-114 and Inferno 29.10-12, the pilgrim’s journey through the afterlife could appear to take a single 24-hour day or it could appear to take 3 full days (amounting to 72 hours by the end if we assume the 12-hour jump at the close of Inferno 34 brings the pilgrim forward in time). The poet appears to have hidden a timepiece in Inferno that, when collected and put together, embodies the trinitarian paradox of being simultaneously three and one.
—
For the sake of completion, I want to include a gloss that clarifies how this passage refers to the afternoon. As detailed in my commentary to Inferno 10.79-81, the full moon occurs when the sun and moon are in direct, 180-degree opposition to one another. I also detailed in that same commentary that the moon moves eastward relative to the sun at a rate of 12 degrees per day. As such, when the moon finds itself at the imum coeli, the sun will be offset to the west of high noon (or the midheaven) by 12 degrees (~1 day) if we use the abbreviated timeline, or by 24 degrees (~2 days) if we use the extended timeline. Considering that the sun covers 360-degrees in a solar day, we want to know how much time is captured by the distance between the sun and the midheaven when the moon is at the imum coeli on the days after a full moon. The calculation is a rather straightforward equivalence that puts the portion of the sun’s motion that interests us in relation to the total motion of the sun in a day.
360 degrees / 24 hours = 12 degrees / x hours
360 degrees * x hours = 12 degrees * 24 hours
360x = 288
x = 0.8 hours
Note that this is not the only way to go about this calculation.
Under a full moon, the sun is at the midheaven when the moon is at the imum coeli. In the days that follow, sun will delay ⅘ of an hour with respect to the moon’s arrival at the imum coeli. Accordingly, the abbreviated timeline would stipulate that Inferno 29.10-12 refers to around 12:48pm, while the lengthier timeline locates this moment around 1:36pm.
Inferno 34.100-139
[diagram]
«Prima ch’io de l’abisso mi divella,
maestro mio», diss’ io quando fui dritto,
«a trarmi d’erro un poco mi favella:
ov’ è la ghiaccia? e questi com’ è fitto
sì sottosopra? e come, in sì poc’ ora,
da sera a mane ha fatto il sol tragitto?».
(Inf. 34.100-105)
This closing section of Inferno is a key passage with respect to the textual presentation of astronomy in the first cantica. The pilgrim’s confusion in the face of the world-reversal that occurs around the midpoint of Inferno 34 is a performance which dramatizes for the reader a series of changes that have occurred as a result of the sudden shift in perspective: 1) the ice of Giudecca is no longer surrounding the pilgrim and his guide; 2) Lucifer now appears upside-down; and 3) it now appears to be morning, whereas it had just previously appeared to be evening (e.g., Inferno 34.68-69: “ma la notte risurge, e oramai / è da partir […],” another example of a Virgilian time reference marked by “oramai”). It is a neat narrative gambit that sets Virgil up to offer an explanation for each point:
Ed elli a me: «Tu imagini ancora
d’esser di là dal centro, ov’ io mi presi
al pel del vermo reo che ’l mondo fóra.
Di là fosti cotanto quant’ io scesi;
quand’ io mi volsi, tu passasti ’l punto
al qual si traggon d’ogne parte i pesi.
E se’ or sotto l’emisperio giunto
ch’è contraposto a quel che la gran secca
coverchia, e sotto ’l cui colmo consunto
fu l’uom che nacque e visse sanza pecca;
tu haï i piedi in su picciola spera
che l’altra faccia fa de la Giudecca.
Qui è da man, quando di là è sera;
e questi, che ne fé scala col pelo,
fitto è ancora sì come prim’ era.
Da questa parte cadde giù dal cielo;
e la terra, che pria di qua si sporse,
per paura di lui fé del mar velo,
e venne a l’emisperio nostro; e forse
per fuggir lui lasciò qui loco vòto
quella ch’appar di qua, e sù ricorse».
(Inf. 34.106-126)
Virgil’s explanation for the pilgrim’s confusion is both simple and fantastic: he has been led across the threshold of the center of the earth, and the shift has wrought a change in perspective that he has failed to recognize. Imagining himself in the northern hemisphere, what he sees cannot make sense; but if the pilgrim imagines instead that he is presently in the southern hemisphere, every complication is resolved. As presented in vv. 118-120, the radical shift in space entails an enormous shift in time: swapping the northern hemisphere for the southern, the implicit observational locus of the fraught astronomy of Inferno jumps across the globe; accordingly, the journey moves through 12 time zones. Scholars have wondered whether this entails shifting forward or backward 12 hours. If opting for the abbreviated timeline, taking Inferno 34.118-120 as a movement backward in time would result in the entire journey spanning 24 hours—morning to morning, from Inferno 1.37-40 to now. If opting for the more prolonged timeline, taking Inferno 34.118-120 as a movement forward in time would result in the entire journey spanning 72 hours from Inferno 1.37-40 to now. Either method of tracking the time is consistent with the totality of textual evidence in Inferno. Finally, Virgil offers here a crucial backstory regarding Lucifer’s fall and how he found himself fixed at the center of the earth in the first place, an apparent retelling of Isaiah 14:12.
All that remains is the end of the first cantica. Importantly, the final verses capture the moment when the pilgrim and his guide finally come to see the sky again for the first time since Inferno 2.
Luogo è là giù da Belzebù remoto
tanto quanto la tomba si distende,
che non per vista, ma per suono è noto
d’un ruscelletto che quivi discende
per la buca d’un sasso, ch’elli ha roso,
col corso ch’elli avvolge, e poco pende.
Lo duca e io per quel cammino ascoso
intrammo a ritornar nel chiaro mondo;
e sanza cura aver d’alcun riposo,
salimmo sù, el primo e io secondo,
tanto ch’i’ vidi de le cose belle
che porta ’l ciel, per un pertugio tondo.
E quindi uscimmo a riveder le stelle.
(Inf. 34.127-139)
The famed final verse of Inferno puts into relief the narrative tension I have been emphasizing with respect to observational astronomy. I have been calling this issue an “epistemic problem” throughout Inferno, and I identified it as a consequence of Inferno 3.22-23, verses which very evidently blot out the skies over Hell. But the final line is, paradoxically, the most emphatic reference in the poem to the dark skies of Hell. The announcement of a return to the stars—“uscimmo a riveder le stelle”—looks ahead to the new poetic content to be found on the shores of Purgatorio while looking back to recall one last time the utter and essential celestial absence of Inferno. All readers will almost immediately feel what is entailed by Dante’s return to the stars at the onset of Purgatorio 1, as the heavens become a key feature of the both the setting and the poetics: “[d]olce color d’orïental zaffiro” (Purgatorio 1.13) is at once the augural image of the entire second cantica, the first observation of the skies since Inferno 1.37-40 and Inferno 2.1, and a contender for the most beautiful stand-alone single line of verse across Dante’s opus. The sweet hue of easterly sapphire, on the heels of the textual return to the stars at the end of Inferno 34, highlights in retrospect how empty and calculated the astral imagery across Inferno was.
The stars of Hell are mechanical, and lifeless. They rarely, if ever, impart a beautiful or inspired image, and they are not rendered in sublime or impressive poetry. I have highlighted repeatedly in my analysis that there is tension caused by Virgil’s apparent observations of the heavens, and I have purposefully left this an unresolved issue because the text never addresses it directly. If we want to speculate about the possible means by which Virgil might know the positions of the stars throughout Inferno, I would propose that he spent those purported “sei ore vuote” between Inferno 1 and Inferno 2 making observations and measurements for Pythagoras and Ptolemy in Limbo who, over the centuries, had fashioned an autonomous timepiece, and they set that timepiece in motion for Virgil (using the data he gathered about the positions of the planets while in the dark wood) when he and Dante passed through Inferno 4. I consider further the epistemic issue of the stars of Inferno in my dissertation. At present, however, I want only to emphasize that the stars circling above Mount Purgatory in the following canto put the darkness of Hell into greater relief. Recalling that, in the context of the poem’s fiction, the narrator’s description of the skies amounts to an approximation of the pilgrim’s memories from the journey, the depiction of the heavens throughout Purgatorio carries a tinge of nostalgia, and this aligns rather beautifully with the larger thematic focus of the cantica. Across Purgatorio the reader finds stunning images of the living sky rendered in equally impressive poetry, and rarely are these passages mechanical time references riddled with equivocation and inconsistency. As the only cantica whose plot takes place on the surface of the earth, Purgatorio represents the only section of the poem where observational astronomy is possible; and under the living, moving light of Mount Purgatory’s skies, the heavens of Inferno look so inert.
–Louis J. Moffa, Jr. (2020-)
Bibliography
Alighieri, Dante. Convivio. ed. Gianfranco Fioravanti. Mondadori, 2019.
Alighieri, Dante. Il Convivio (The Banquet). trans. Richard H. Lansing. Garland Library of Medieval Literature, 1990.
Boccaccio, Giovanni. Esposizioni sopra la Commedia. ed. Giorgio Padoan. Milano, Mondadori, 1964. 11.83, pp. 557-558
Buti, Giovanni, and Renzo Bertagni. Commento astronomico della Divina Commedia: rassegna analitica con una parte generale sistematica e una appendice critica. Sandron, 1966.
Isidore of Seville, Saint. Isidori Hispalensis Episcopi Etymologiarum Sive Originum Libri XX. ed. W. M. (Wallace Martin) Lindsay. Clarendon Press, 1911.
Isidore of Seville, Saint. The Etymologies of Isidore of Seville. ed. and trans. Stephen A. Barney, W. J. Lewis, J. A. Bach, and Oliver Berghof. Cambridge University Press, 2006.
Latini, Brunetto. Il Tesoro di Brunetto Latini. Luigi Gaiter, P. Chabaille, and Bono Giamboni. G. Romagnoli, 1877
Minos, Scott. “International Dark Sky Week.” Energy.Gov, 28 Mar. 2022.
Moore, Edward. Time-References in the Commedia and their Bearing on the Assumed Date and Duration of the Vision. Nutt, 1877.
Plato. “Timaeus” in Complete Works. eds. John M. Cooper and D. S. Hutchinson, Hackett Pub, 1997. pp. 1224–1291
Recommended Citation: Moffa, Jr., Louis J. “Astronomical Diagrams of Inferno.” Digital Dante. Columbia University Libraries, 2020. https://digitaldante.columbia.edu/moffa-inferno/
 Return to top
Return to top